
传统的热力学,也就是非相对论性的热力学,一直以来都是很多人心上的痛,相信很多传统热力学的初学者都会提出很多的问题,这些问题往往会触及到传统热力学的弱点上。
一个非常经典的问题就是:运动物体的温度会不会变?是速度越高温度越高,还是相反,抑或是不变?
前段时间算metric,读了一些资料,摸索了一下,总结了算metric的一般方法,下面的这个方法当然只对natural coordinate system才有效,而且例子中是正交的坐标系。更一般的方法可以使用form来做,这个会在后面的form的笔记中提到。 Let’s check the definition of metric again. 长程相关: 天体周围引力场和 Birkhoff 定理 外微分形式 | {Differential Forms} [1] 外微分形式 | {Differential Forms} [2] 李导数和Killing矢量场 | Lie Derivative, Killing Vector Field
Lie derivative(读音/li:/)翻译为李导数,是与协变导数(covariant derivative)不同的一种导数。简单的说,Lie derivative是用来比较流形上两个不同点的张量的不同的,或者说,是用来衡量张量场沿着曲线族移动时的变化的,再或者说,是用来描述流形上的张量场被沿着矢量场(或者说是曲线的切矢场)拖拽时的变化的。

The 2011 Nobel Prize in Physics is awarded “for the discovery of the accelerating expansion of the Universe through observations of distant supernovae” with one half to Saul Perlmutter and the other half jointly to Brian P. Schmidt and Adam G. Riess.
目前大家的观点,除了那些分析实验出了问题的文章(eg,synchronisation),其他的承认实验数据的精准性的大致包括如下观点:
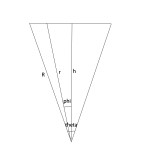
昨天我大致浏览下,发现没有考虑baseline上不同地方的万有引力不同所带来的效应。但是这个效应是使得中微子提前到达,不过还是算了下。发现完全可以忽略的。不过作为一个练习,我还是把这个贴出来,以备查阅。
1. In \(\mathsf E^3\), \(\vec x\) is an a point described by \(\mathrm d \vec x=\sigma_1\hat e_1+\sigma_2\hat e_2+\sigma_3\hat e_3\). It should be made clear that \(\sigma_i\) are 1-forms and \(\hat e_i\) are bases. In fact, \(\mathrm d\vec x\) is a 1-form here.
1. Exterior derivatives are mappings from smooth manifold \(\mathcal{M}\), which is m dimensional, to itself, that satisfy the following conditions.




最近评论