中微子比光快实验中的引力效应分析

论文在此：
http://arxiv.org/abs/1109.4897(Measurement of the neutrino velocity with the OPERA detector in the CNGS beam)

昨天我大致浏览下，发现没有考虑baseline上不同地方的万有引力不同所带来的效应。但是这个效应不是使得中微子提前到达，不过还是算了下。发现完全可以忽略的。作为一个练习，我还是把这个贴出来，以备查阅。

所用到的参数如下(长度单位都是km，时间单位都是s，质量单位都是kg)：

\begin{eqnarray}
\rho &=& 5515.3*10^9 \\
G &=& 6.67 * 10^{-11} 10^{-9} \\
R &=& 6357 \\
\theta &=& 0.0115 \\
h &=& R cos(\frac{\theta }{2}) \\
M &=& \frac{4}{3} 3.1416 r’^3 \rho \\
r &=& \frac{h}{cos(\phi)} \\
c &=& 300000
\end{eqnarray}

（基线长度:\(L=732\)，这样算出来的整个baseline所对应的圆心角\(\theta\)，因为计算时用到\(\theta\)所以我直接算出来放在上面的参数列表了。）

各个物理量的物理意义见下图（最上面的横线是baseline）和下述说明：

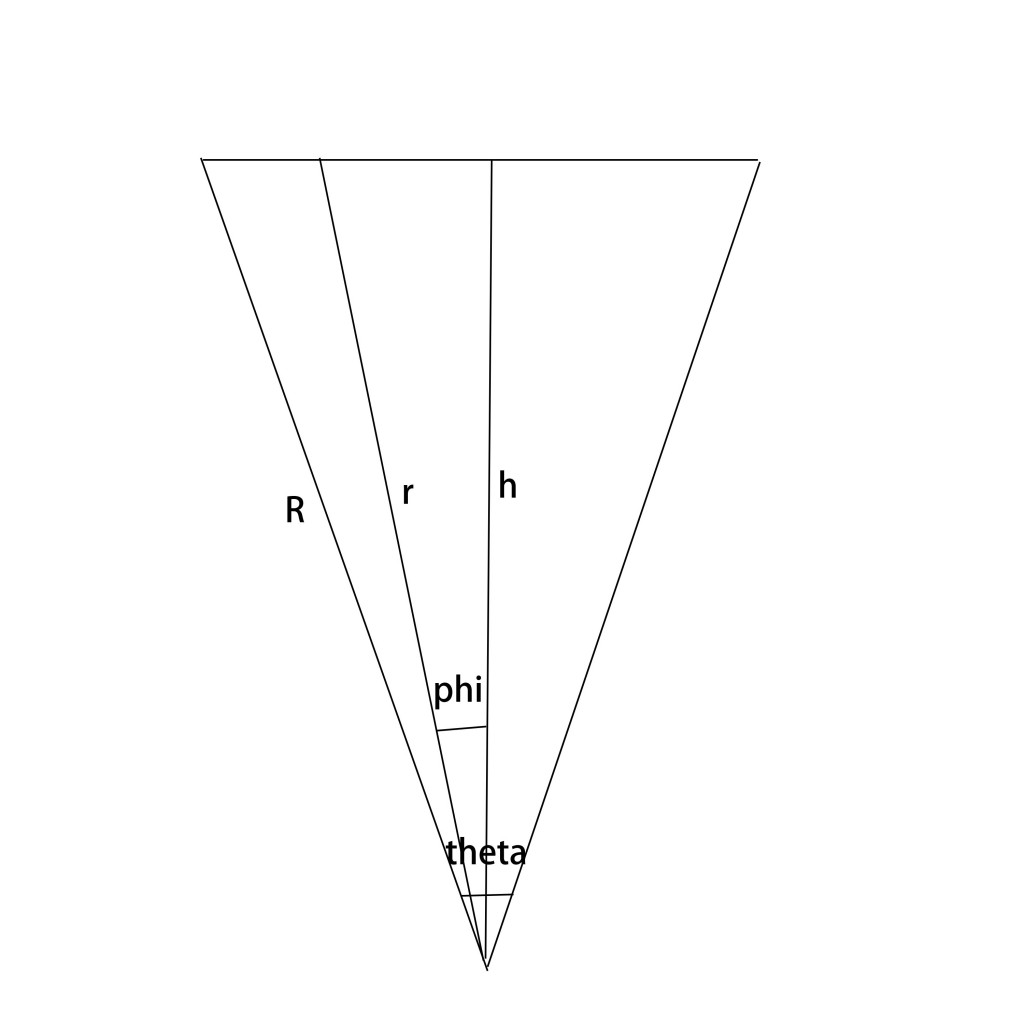
\(G\)为万有引力常数，\(\rho\)为地球密度（其实这个可以不用到，但是为了减少中间公式变形的次数，就姑且用一下吧）,\(M\)为地球质量，\(c\)为光速，\(R\)为地球半径。

假设中微子是类光粒子，那么有\(\mathrm ds^2=0\)。那么根据Schwarzschild度规的线性近似，
\begin{equation}
\mathrm ds^2=(1-\frac{2M}{r})\mathrm dt^2-(1+\frac{2M}{r})\mathrm dr^2-r^2\mathrm d\theta^2
\end{equation}

这样可以作如下积分来计算类光粒子粒子穿过一段距离的时间.
首先按照准确的算，就是说路径上的引力会变：
这样要把上面参数\(M\)里面的\(r’\)设置成\(r\)
\begin{eqnarray}
2 \text{NIntegrate}\left[\sqrt{\frac{1+2 M \frac{G}{r\text{ }c^2}}{1-2 M \frac{G}{r c^2}}\frac{1}{c^2}\left(\frac{h}{\text{Cos}[\phi ]}\right)^2+\frac{(h \text{Tan}[\phi ])^2}{c^2 \left(1- 2 M \frac{G}{r c^2}\right)}},\left\{\phi ,0,\frac{\theta }{2}\right\}\right]
\end{eqnarray}
这样算出来的结果是：
0.00024368365750689964

然后把\(M\)里的\(r’\)设成常量\(R\)
\begin{eqnarray}
2 \text{NIntegrate}\left[\sqrt{\frac{1+2 M \frac{G}{r\text{ }c^2}}{1-2 M \frac{G}{r c^2}}\frac{1}{c^2}\left(\frac{h}{\text{Cos}[\phi ]}\right)^2+\frac{(h \text{Tan}[\phi ])^2}{c^2 \left(1- 2 M \frac{G}{r c^2}\right)}},\left\{\phi ,0,\frac{\theta }{2}\right\}\right]
\end{eqnarray}
结果是：
0.00024368365750691075

最后算一下时间差值：
0.00024368365750689964 – 0.00024368365750691075=-1.11131*10^-17

符号的意思是说，中微子真正所花掉的时间要比按照常引力算的时候要少，因为baseline中点在地球内部，那里的引力小，导致时间比地面快些。

好吧，小计算。Mathematica文件在此（我太懒了只好用Mathematica了）：GRwithNeu

Cahill在算group velocity的影响。等下看结果吧。