上周 colloquium 的时候,第一次听到 quaternion 这个词,觉得很新鲜。quaternion 的矩阵表示是 长程相关: 量子力学计算的一个小技巧 爱情的量子理论2 外微分形式 | {Differential Forms} [1] 外微分形式 | {Differential Forms} [2]
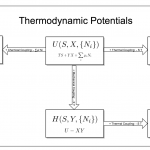
今天办公室有个人跟我说她总是记不住 thermodynamic potential 之间的关系。于是我就给她讲了 Legendre transformation. 我想了想,热力学势(特性函数)可以总结成下面的一张图。 这篇文章就是简要的解释一下这张图。这篇文章只是给热力学的初学者看的,如果你已经学过理论力学或者统计物理的,我就是在浪费你的时间了。 长程相关: Hubble膨胀,Galilean-invariant,non-equilibrium How to construct the metric tensor? Relativistic Thermal Dynamics | 相对论性热力学 心理叠加态:从量子爱情到人的所有心理
线性代数里面我们的矩阵一般是求解方程组引入的。 那么除了求解方程组之外,线性代数还可以做什么呢? 我们高中学过的线性规划,实际上也可以归结为线性代数问题,里面比较著名的一个方法是单纯形法。那么我们高中学过的几何呢?能不能也用线性代数来解决一些几何的问题呢? 长程相关: 推荐:话说微积分 一页纸上的微积分
我们都说微分和积分是一对互逆的运算,那么究竟怎么个互逆法呢? 花了点时间把微分和积分的相应内容列举出来了: 长程相关: 推荐:话说微积分 线性代数与几何
前段时间算metric,读了一些资料,摸索了一下,总结了算metric的一般方法,下面的这个方法当然只对natural coordinate system才有效,而且例子中是正交的坐标系。更一般的方法可以使用form来做,这个会在后面的form的笔记中提到。 Let’s check the definition of metric again. 长程相关: 天体周围引力场和 Birkhoff 定理 外微分形式 | {Differential Forms} [1] 外微分形式 | {Differential Forms} [2] 李导数和Killing矢量场 | Lie Derivative, Killing Vector Field
1. In \(\mathsf E^3\), \(\vec x\) is an a point described by \(\mathrm d \vec x=\sigma_1\hat e_1+\sigma_2\hat e_2+\sigma_3\hat e_3\). It should be made clear that \(\sigma_i\) are 1-forms and \(\hat e_i\) are bases. In fact, \(\mathrm d\vec x\) is a 1-form here.
1. Exterior derivatives are mappings from smooth manifold \(\mathcal{M}\), which is m dimensional, to itself, that satisfy the following conditions.
从今天开始,会不定期的贴出比较完整的外微分形式(exterior differential forms)的大纲。大部分只是简单的从书本中摘出来的,以便以后快速回想和查阅使用。初学者可能会犯很多错误,强烈要求指正。 所读书本为Harley Flanders的书,Google Books链接在文末给出。 长程相关: 外微分形式 | {Differential Forms} [2] 外微分形式 | {Differential Forms} [3] How to construct the metric tensor? 天体周围引力场和 Birkhoff 定理
最近评论