2011年诺贝尔物理学奖

2011年诺贝尔物理学奖

· by · in

The 2011 Nobel Prize in Physics is awarded “for the discovery of the accelerating expansion of the Universe through observations of distant supernovae” with one half to Saul Perlmutter and the other half jointly to Brian P. Schmidt and Adam G. Riess.

“中微子事件”论文汇总 | Speeding Neutrino Task Force

· by · in

目前大家的观点，除了那些分析实验出了问题的文章(eg,synchronisation)，其他的承认实验数据的精准性的大致包括如下观点：

收入支出及其它

收入支出及其它

· by · in

今天突然兴起去算了一下自己一个月的消费，意外的发现原来作为学生其实消费也不是很高的嘛，作为一个对照，我把我的收入也贴出来了，放在最后 2011年8月26日到9月26日的消费状况，最后一行是总消费，最后一列是卡余额（呃这个没用），勤工助学中心在这里其实大部分情况下是本部超市： 长程相关: Fight Against sth 百篇纪念 公理体系的世界 | First Principle 一个「精神病人」的救赎

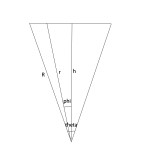
中微子比光快实验中的引力效应分析

中微子比光快实验中的引力效应分析

· by · in

昨天我大致浏览下，发现没有考虑baseline上不同地方的万有引力不同所带来的效应。但是这个效应是使得中微子提前到达，不过还是算了下。发现完全可以忽略的。不过作为一个练习，我还是把这个贴出来，以备查阅。

外微分形式 | {Differential Forms} [3]

· by · in

1. In \(\mathsf E^3\), \(\vec x\) is an a point described by \(\mathrm d \vec x=\sigma_1\hat e_1+\sigma_2\hat e_2+\sigma_3\hat e_3\). It should be made clear that \(\sigma_i\) are 1-forms and \(\hat e_i\) are bases. In fact, \(\mathrm d\vec x\) is a 1-form here.

外微分形式 | {Differential Forms} [2]

· by · in

1. Exterior derivatives are mappings from smooth manifold \(\mathcal{M}\), which is m dimensional, to itself, that satisfy the following conditions.

理想流体引力体系的熵最大原理 ｜ arxiv:1109.2804

· by · in

A General Maximum Entropy Principle for Self-gravitating Perfect Fluid Author: Sijie Gao Date:September 14, 2011 arXiv:1109.2804 Category: GR-QC 这是一篇读起来非常简单的文章，作者把推导过程写的很详细，而且只要学过统计物理，文章所讨论的内容和使用的方法就很容易理解。 这篇文章使用熵作为作用量，导出了引力体系的熵最大原理。文章的导出过程中，使用了一些技巧，例如求变分极值很自然的使用Euler-Lagrange方程，不好用的constrain使用Lagrange multiplier方法把constrain引入进来等等。使用这个最大熵原理可以导出TOV方程。 长程相关: Hubble膨胀，Galilean-invariant，non-equilibrium Relativistic Thermal Dynamics | 相对论性热力学 我们的宇宙可能由闭宇宙演化为开宇宙么？[小结] 关于暗能量那些稀奇古怪的名字

Eclipse + CDT | Gedit plugin

· by · in

此文仅用于存档。 一 Eclipse + CDT 前些日子见到师兄用的编辑器可以查找函数变量等的declaration，很是新奇。于是照师兄所说，也装了eclipse。 一开始感觉非常糟。我用的编辑器都是很简单的，vim，gedit，gummi等，看起来清爽，也从来不会用什么自动完成，自动加括号，自动缩进什么的，觉得这些事情都是要自己干才放心。 长程相关: 美丽的TeX： texample.net | txt2tags.org | S5 Online Html+Mathjax Editor Typography Prezi by Travis Hitchcock 宇宙各成分之间关系 | Tikz和PGF