Q: Using the simplest program to calculate the 2D Ising model upon triangle lattice.
[eq]H=J\sum\limits_{i,j}{{s_{i}}{s_{j}}}[/eq]
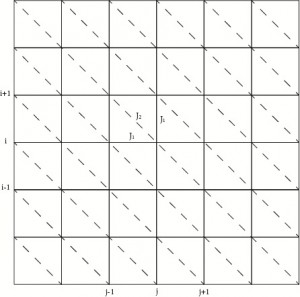
2. Lattice:
Fig3-Triangle-2D-Ising
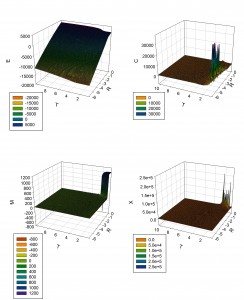
3. Summary image:
2D_Triangle_Ising_Model
——CODE&SUMMARY——
*PDF file (some results shown in it):
2D_Ising_Model(Triangle)
(A little reminder: I am not really working on this kind of things. The only reason I did this is that I have to hand in a copy of my homework. So IF U R LOOKING FOR SOME REAL INSPIRING CODES, NEVER STUDY MINE!)
*CODE file (html):CODE_2DIsingModel-Triangle
My CODE is appended here:
#include
#define L 32
int sum_M;
struct Obsv
void Inist();
int main()
R=R_i;
void Inist()
void MCP(double R)
sum=s[i][j]*(s[(L+i-1)%L][j]+s[(i+1)%L][j]+s[i][(j-1+L)%L]+s[i][ (j+1)%L]+R*(s[(i+1)%L][(j-1+L)%L]+s[(i-1+L)%L][(j+1)%L]));
dE=2*sum;
struct Obsv Cac_obsv(double R)
for(i=0; i
return emcx;
void Mag()
void Energy(double R)

最近评论