Draft ( PDF file, click to view or download):Frustrated-Honeycomb Heisenberg-Model
We did not do much on this because of the limitation of time.
Here we have some slides to show the main idea of this work.2D_Honeycomb_Frustrated_Heisenberg_Model_Monte Carlo
Codes:Honeycomb-2DIsingModel Rigid-Honeycomb-2DIsingModel Visual-Honeycomb Final-pirntspin-Honeycomb Rvaries-Triangle-2DIsingModel
============= Divider of Main Text================
[eq]H={{J}{1}}\sum\limits {i,j}{{{s}{i}}{{s} {j}}}+{{J}{2}}\sum\limits {i’,j’}{{{s}{i’}}{{s} {j’}}}[/eq]
,in which i,j means the nearest neighbor interaction when i’, j’ means the next nearest neighbor interaction.
We designed the program under Honeycomb lattice, i.e.,
Scheme of a honeycomb lattice
To make it clear for programming, we reshaped the lattice under homeomorphic:
Transformation of honeycomb lattice for MC program
I wrote the Metropolis CODE with C:/This program calculates the energy, heat capacity, magnetization, magnetic permitivity. /Boundary condition: periodic boundary condition. /In this program, J&k are put into T. To fill it to the expressions, just consider the dimensions. /
include
include
include
include
#define L 100
double sum_M[2]; /*sum_M[0] denotes the cos part; sum_M[1] denotes the sin part*/
struct Obsv
/********************************/
void Inist();
int main()
R=R_i;
void Inist() /*Initialized lattice. All oriented to one direction*/
struct Obsv Cac_obsv(double R)
Mag();
for(i=0; i
return emcx;
/*Monte Carlo process.*/
/*Cal the energy before we add a random angle to s[i][j]*/
/*Add a random angle to s[i][j]*/
/*Cal the energy after we add a random to s[i][j]*/
/********************************/
if(dE< =0)
}
/********************************/
void Mag()
// for(i=0;i
/********************************/
void Energy(double R)
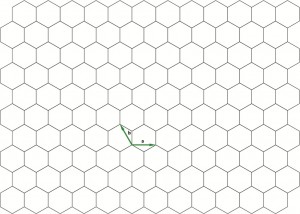
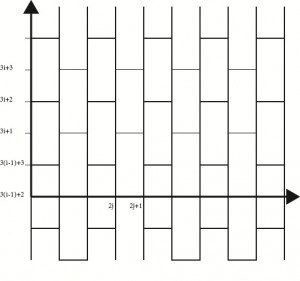

、请问将honeycomb lattice 做拓扑变形是什么意思?为什么就简化了呢?
呃,因为写程序的时候,直接生成honeycomb是比较麻烦的,所以要变成格点所处位置是正方格子的位置,这样可以简单的用矩阵表示。体系的性质跟它的具体的形状没有关系,体系的性质在交换作用系数和最近邻次近邻的个数里面给出了,所以我就把它压扁成这个了~
谢谢。很好的思路。这就相当于把honeycomb 给拉直了。以前看到过别人这么处理kagome lattice的,一直不懂,今天终于理解了。请问拓扑变形这方面的文献啥的有没有?
文献我还真没有。我这个只是一个小作业,所以也没看多少文献……