Evolution of Background and Perturbations in {Cosmology} [Details]

|This is a Cosmology Series.|

Contents
Background
Perturbations

This is a general introduction to the evolution of the universe with one figure.

In the previous post, I attached two figures. Now we will go into the details.

Background | _{Back to contents}

The first figure divides the diagram into several areas. (We might regard the different areas as different phases of the universe.)

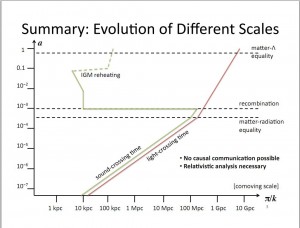
Borders

Matter radiation equality.
The moment when the density of matter and the density of radiation are equal.

Recombination (of electrons and protons).
Energy/temperature drops far below \(\epsilon_0=13.6\text{eV}\) and hydrogen produced.

Matter Λ equality.
The moment when the density of matter and the density of cosmology constant Λ are equal.

The green line is the sound-crossing time.
Sound speed \(c_s\) here is defined as \(\delta p=c_s^2 \delta \rho\).
a. The sound spread quickly at first because the universe is a bowl of photon baryon soup. It drops after matter radiations equality because matter turns out to be less relativistic and the effective pressure becomes smaller.
b. At the moment of recombination, it drops dramatically. Is it because the recombination cut the trace of the sound into pieces and makes the sound hard to spread to large scales?
# What is recombination? Roughly speaking, it is the era when the temperature of the universe is low enough to let the electrons and protons combine.

The red line is the light-crossing time.
This is defined as the time light needs to cross a certain distance. In other words, it is largest distance that light travels starting from the origin of the coordinate we use.
a. The line in the figure is not so accurate because it should never be a polygonal line. The universe transits from radiation domination to matter domination gradually.

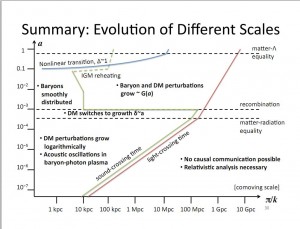
Perturbations | _{Back to contents}

Areas/phases

Dark matter (DM) perturbations grow logarithmaticlly.
In radiation era \(\delta_m=C_1+C_2 \ln{t}\).

Acoustic oscillations.
In radiation domination (RD), baryon-photon fluid obeys,
\begin{equation}
\frac{\partial^2\delta}{\partial t^2}-\frac{c_s^2}{a^2}\Delta^2\delta -4\pi G a \bar{\rho}\delta + 2 H \frac{\partial \delta}{\partial t}.
\end{equation}
This equation is a damped wave function. Exact solutions with some certain boundaries and initials conditions can be calculated.

Relativistic analysis is need on large scales in RD.
Jeans length (characteristic length of spreading of the sound waves) is
\begin{equation}
\lambda_J=\sqrt{\frac{32}{3}}\pi /\frac{a}{c_s t}
\end{equation}
During RD, plasma of photon and matter has a sound speed of \(c_s=c/\sqrt{3}\). Then \(\lambda_J=\frac{4\sqrt{2}\pi}{3}\frac{c t}{a}\), which is larger then the distance light can travel.
That is because when we do the calculation, general relativity effects are not concerned.

Baryon smoothly distributed.
In matter domination (MD), potential is dominated by dark matter. The evolution eqn for baryons is \(\ddot{\delta_b}+2 H \dot{\delta_b}-\frac{c_s^2k^2}{a^2}(\delta_b+\frac{\Phi}{c_s^2})\).
a. For scales \(k \gg a/c_s t\), the sound wave quickly shakeout the perturbations. Equivalently speaking, the third term dominates the equation. So the solution for it is \(\delta_b=-\frac{\Phi}{c_s^2}\).
b. For scales \(k \ll a/c_s t\), the sound waves hardly affects the perturbations. Equivalently speaking, the terms \(\ddot{\delta_b}+2H\dot{\delta_b}\) dominate the equation. The solution to this is just as the same as the dark matter, \(\delta_b=C_1+C_2 \ln{t}\).