热力学势

• Legendre Transformation
• Coupling
• 图片的诠释
  • Maxwell 关系
• Legendre Transformation Revisited
• 微分几何

本科学习的热力学主要的内容包括下面几部分（参考 A Modern Course in Statistical Physics by L. E. Reichl）：

1. Thermodynamic variables; extensive, intensive, neither;
2. Equations of state;
3. Four fundamental laws of thermodynamics;
4. Thermodynamics potentials
5. Phase transitions
6. Response
7. Stability

整个的思路跟 mechanics 类似。先搞清楚如何描述一个体系，包括状态和”kinematics”，这里 “kinematics”包括状态方程和特性函数。其次，提出“第一性原理”：四条热力学定律。然后研究“动力学”：相变、响应和稳定性。

而这里面热力学势的关键除了搞清楚每个势的意义，另外就是要搞清楚哪些是变量。而确定哪些是变量的就是 Legendre transformation. 所以，要搞清楚这些势，可以从 Legendre transformation 下手。

热力学势（特性函数）可以总结成下面的一张图。

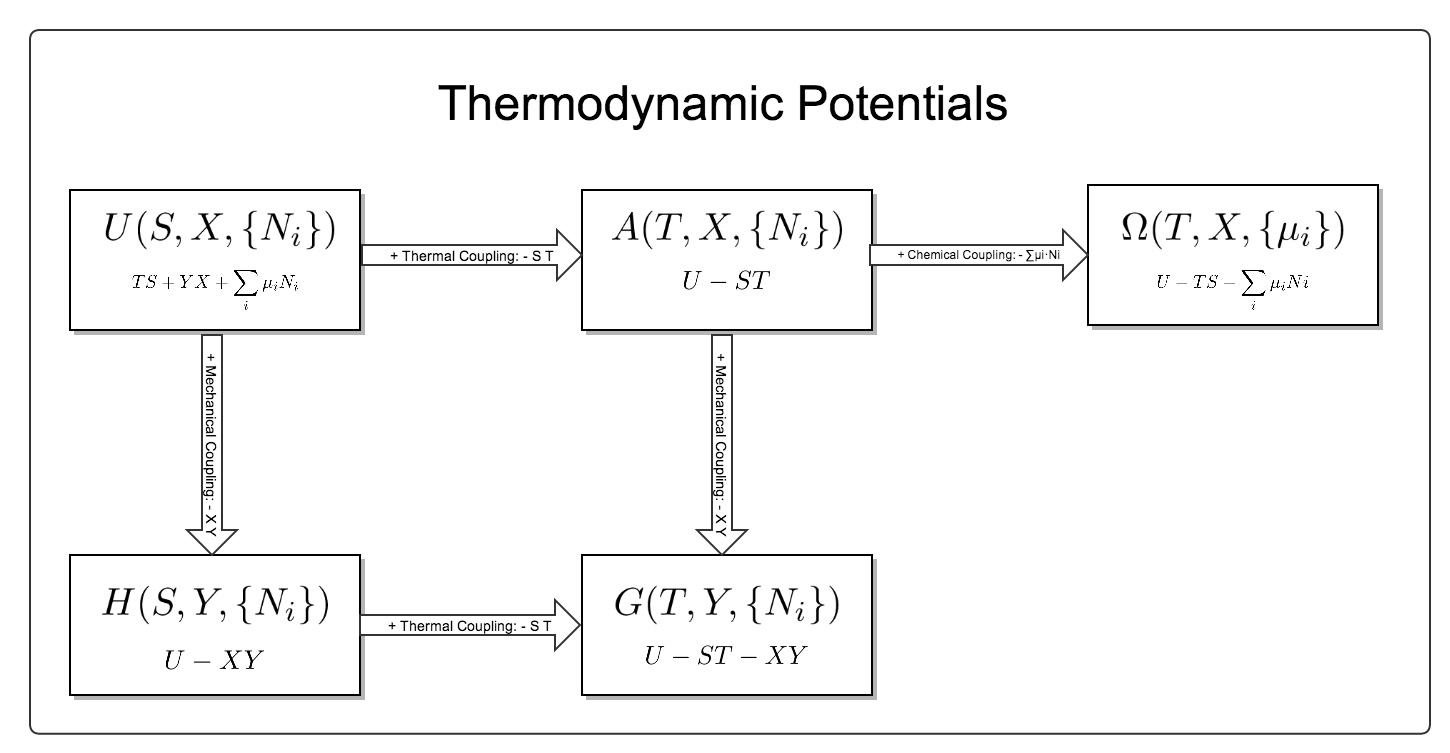
这篇文章就是简要的解释一下这张图，以及 Legendre 变换。

Legendre Transformation

Legendre transformation 的基本定义在《经典力学的数学方法》中有，我写过一篇简单的笔记，当时总结的不是很清楚，而且如果仅仅是为了比较肤浅的理清楚热力学势的关系，不太需要很严格的定义。所以我重新功利的说一下。

如果我们有一个函数 $U(T)$，其中 $T$ 是自变量，而我们想要得到另一个函数 $H(S)$，自变量变成了 $S$，那么在热力学势的范围内，我们只需要做这样的变换：

\[H(S) = U -TS\]

当然，这个变换跟书里面的 Legendre transformation 差一个符号，这个并不重要，定义成差一个负号，更加符合物理的理解，因为这些都对应的能量，增加一个量看能量的变化，如果加了负号，增量正好相反，反而不便。

这样我们说 $U(T)$ 和 $H(T)$ 对偶。（在 mechanics 里面，Lagrangian 和 Hamiltonian 也是对偶，理论力学里面最最重要的一个关系之一。）

Coupling

图片里面提到了三种不同的 coupling：

1. Thermal Coupling: $-TS$
2. Mechanical Coupling: $-YX$
3. Chemical Coupling: $-\sum_i \mu_i N_i$

其中 $Y$ 是广义力（例如压强 $p$ ），$X$ 是广义位移（例如体积 $V$ ）¹。这个也不需要很多解释吧，深刻的解释我也没用，总之，顾名思义。

图片的诠释

现在可以开始解释图片的意思了。首先解释各个符号的意思：

1. $U$, $H$, $A$, $G$, $\Omega$ 分别是：内能，焓，Helmholtz 自由能，Gibbs 自由能，巨热力学势。
2. {$S$, $T$}， {$X$, $Y$}， {${N_i},{\mu_i}$} 分别是：{熵，温度}，{广义位移，广义力}， {粒子数，化学势}。
3. 三种 coupling 上面已经解释了。

整个图片是从中间的 $U(S,X,{N_i})$ 开始的，这是内能，内能是熵S、广义位移 X （以及粒子分布 {N_i} ）的函数。。

1. 如果我们给内能 $U(S, X, {N_i})$ 加上一个 mechanical coupling $-XY$，那么就得到了焓。从前面的 Legendre transformation 看到，这时候焓 $H$ 变成了 $S, X, {N_i}$ 的函数。所以在气体的理论中，$H$ 是 $S, p$ 的函数，所以等压热容自然是 $C_p = \left( \partial_T H\right)_p$.
2. 如果我们给内能和焓加上 thermal coupling $-ST$，那么我们就得到了两种自由能，分别是 Helmholtz 自由能和 Gibbs 自由能。同第一条里的道理，可以通过 Legendre transformation 自行分析两个是什么的函数。
3. 如果我们给 Helmholtz 自由能加上一个 chemical coupling $-\sum_i \mu_i N_i$，那么我们得到了巨热力学势 $\Omega(T,X,{\mu_i})$。

至于物理意义，从图上也很明确。例如焓 H 是内能去掉 mechanical coupling，也就是说，焓在不考虑机械功的时候好用，例如焓在考虑其他体积不变的时候好用，因为这时候吸热就是焓。其他的也是同样的方式理解。这样我们仅仅通过内能 $U(S, X, {N_i})$ 和 Legendre transformation 就可以获得其他的热力学势。

Maxwell 关系

内能 $U(S,X,N)$ 出发，根据不同的 coupling，我们可以导出不同的热力学势是什么的函数（也可以通过 Legendre transformation，这里简单起见只利用图片来做）。例如，H 是什么的函数？$U(S,X,N)$ 我们去掉了 mechanical coupling -YX 那么 得到的 H 就是 $H(S,Y,N)$，因为勒让德变换 $H = U - YX$ ，原来是变量 X 的函数，要变成 Y 的函数。

我们知道了这些函数的自变量是什么，下一步就可以写出所有的热力学势的微分式。只举一个例子：

\[\mathrm d U(S, X) = T\mathrm d S + Y \mathrm d X\]

然后，我们可以写出这些热力学势的全微分（由偏微分表示的，就是 chain rule）。同样只举一个例子：

\[\mathrm dU(S, X) = \left(\frac{\partial U}{\partial S}\right)_X \mathrm d S + \left(\frac{\partial U}{\partial X}\right)_S \mathrm X\]

对比上面两个公式，可以得到两个式子，分别是

\[T = \left(\frac{\partial U}{\partial S}\right)_X\] \[Y = \left(\frac{\partial U}{\partial X}\right)_S\]

用同样的方法得到由另外的热力学势表达的 $T$ 和 $Y$，这样就可以获得一组 Maxwell 关系式。然后用类似的方法处理所有的热力学势，就可以获得全部的 Maxwell 关系。

另外，我们看到热力学量可以通过对相应的热力学势求偏微分来获得，很方便。

这个推导在物理中很常见，例如电动力学的学习中，磁场能的导出也是用类似的手段。

Legendre Transformation Revisited

上面除了图片有点物理之外，就是数学了，或者说就是 Legendre transformaton 了。一开始那个 Legendre transformation 看起来就是硬生生的代数呢，感觉并没有什么直观的意义？其实这个 transformation 背后有很多可以挖掘的，包括我们喜欢的简洁明了的图像。

我们换种方式来找出函数 $f(x)$ 的 Legendre 变换。

1. 把函数在 x-y 坐标系中画出来（蓝色的实线）。
2. 做一条直线 $y=px$ .
3. 我们现在可以定义一个距离，也就是做一条垂直 x 轴的直线，在 $y=px$ 和 $f(x)$ 上的两个交点的距离： $F(x,p) = xp - f(x)$. 现在看起来已经有了 Legendre transformation 的样子了。但是有个问题，这里 x 和 p 是两个独立的变量。
4. Legendre transformation 要求在给定一个直线斜率 p 之后，这个距离 $F(x,p)$ 最大。这样就确定了 x 和 p 的关系。也就是说要求 $\frac{\partial F(x,p)}{\partial x} = 0$，简化之后，$f’(x)=p$。如图所示。
5. 这样把 x 和 p 的关系 $x(p)$ 代入 $F(x,p)$ 中，我们的距离就变成单单 p 的函数，$F(p)$ 。这就是 $f(x)$ 的 Legendre transformation.

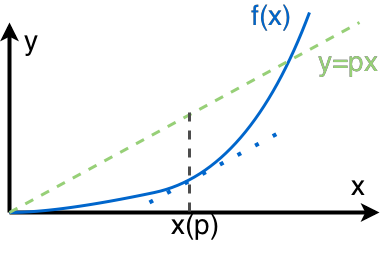
这里面的几何关系就是，$p$ 是斜率，$f’(x)$ 也是斜率。

说到这里还不够清楚，那么我们重写一下这个关系：

\[F(p) + f(x) = xp\]

嗯？非常简单粗暴：$f(x)$ 和 $F(p)$ 具有对称性。等一下，这个关系联想到了什么？我们把上图中的表示切线的点划线延长出来，

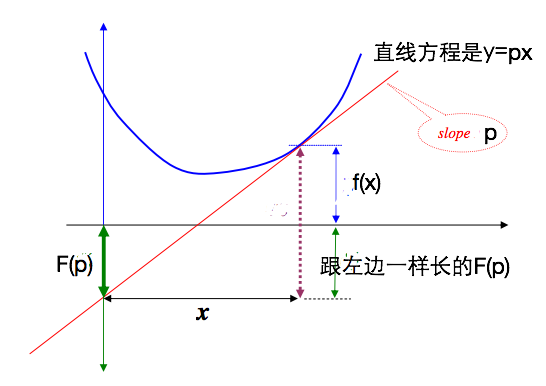
从这个图上，明显的就是斜率 p 乘以 x 得到了 $f(x) + F(p)$，即

\[f(x)+F(p)=p x\]

简单明了吧。这就是 f(x) 和 F(p) 之间的 Legendre transformation .明显的这个变换具有对称性，因为 f(x) 和 F(p ) 的地位相同。

至于更多的关于这个变换的内容，可以参考《经典力学的数学方法》这本书，或者这篇文献。这是物理上一个非常核心的变换，对于整个物理体系有很重要的作用。

微分几何

上面的这些东西，是我们本科学习的，我们会觉得好乱！是的，好乱！那是因为我们使用的数学语言很含糊。我们为什么要说一个量是什么什么的函数？因为我们想要求导数。

如果我们有一种方法，可以得到导数的含义，但是不需要指定一个量是什么什么的函数，那么上面的这些混乱就没有了。是的，这种方法就是外微分。

至于具体怎么理解这个问题，可以读一下这篇文章。