爱情的严格量子力学描述

[Update:03-21]

Actually, I am joking! DO NOT PANIC! 本文弃用 CC 协议。不许转载。因为文章还没成型，我只是把我的所有的尝试都写在这里。而且，记着所有这些都是笑话而已。本文将已经完成于2200AD。

第一章 问题的引入

生平最恨不幸的故事入耳。

幸与不幸，我没有评判标准，所有的测量全部需要在故事主人公的参考系进行。在故事主人公的情感与观者的情感无冲突的情况下，主人公的情感就仅仅是一个标量，故事主人公自身参考系中当时当地的幸，任何平移下都不变。然而，为了描述故事主人公的幸与不幸，我们需要找出能够代表某种情感的可以量化的参量，一般此参量是特定情感下的所有的人共有的一种可以度量的表现，或者故事主人公所特有的一种表现。比如下面在分析爱情的时候所采用的其他观者远离自己的快慢程度（自己与其他观者的有效交流的多少）乘以其他观者的弥散程度（其他观者对于自己的重要程度）。

有两件事情可能是非常复杂的。

其一是存在耦合的情况。如果故事主人公的感受是与其他观者耦合的时候。这种情况往往会导致无穷递归的情况。倘若也是下面将要提到的含时的情况，那么还可能会出现混沌的情况。这部分情况需要以后进行细致讨论。

其二是含时的测量。举例来说，一个当地观者想要观测自身参考系中的爱情感受进行描述。由于心理学的相对性原理，人所感受到的时空背景不仅仅与物理的时空有关，还与观者自身的情感状况（情感密度和情感的物态方程）有关，于是感受的强烈程度会导致心里时空背景的扭曲。这部分可以通过场方程来描述。

\[G_{ab}=GT_{ab}\]

其中，$G_{ab}$ 是描述时空背景的张量；$T_{ab}$ 是描述感受的张量；而有趣的是标量 $G$，它描述了情感密度对心里时空的影响的程度，在经典近似下，可以看作情感密度与心里时空扭曲标量的比值。

为了方便对事件的描述，我们引入 conformal time 的概念。conformal time 就是指的观者在某情感状态下的心理时间。这个量并没有可用的明确定义，所以在使用之前需要实现定义。比如我们一般喜欢定义当前情感状态下的时间为 conformal time，记作 $\tau(t)$。括号里面的变量意味着这个因子是与心理时间相关的。这样的话，对于一个含时的问题的描述，我们需要引入因子a，心理时间与 conformal time 之间的换算关系为 $t=a\tau$。 实验上，我们可以通过下面的定义来给出a。

\[H(t)=\frac{\mathrm d a/\mathrm d t}{a} .\]

其中，$H(t)$ 是心理弥散常数。从定义可以看出，$H(t)$ 的意义是，在观者自身参考系所观测其他观者时，所测量到的其他观者远离自己的快慢程度和其他观者的弥散系数的合作用的结果。其他观者远离观者的速度越快，$H(t)$ 就越大；其他观者相对与观者的弥散程度越大，$H(t)$ 就越大。

我来解释一下其他观者远离自己的快慢程度。这个常常被描述成主人公远离其他人的速度，在我们这里，因为所有的观测必须先在故事主人公的参考系完成，所以这样描述是不太方便的。其他观者远离自己的速度应该怎么描述呢？我们需要引入红移，即 redshift。Redshift 是描述观者在接收到其他观者的一个试探(probe，可能是一个问题，一个碰触，总之是某种意图引起故事主人公注意的行为)之后，给出回应（respond）并最终接受到其他观者能够证明已经接受到该回应的回应的这个过程所需要的时间，这个时间是用心理时间来衡量的。这样来说，其实红移并不是一个很方便测量的量。为了能够测量，我们需要将这个过程所需的心理时间归一化，归一化常数就是在前面选定confomal time时所选定的那个作为标准的情感状态下这个过程所需要的时间的倒数，并且为了以后更好用，还要减去1。即，

\[z=\frac{t_a}{t_0}-1 .\]

另一个需要给出解释的量是弥散系数。上面提到的红移并不能完整的描述故事主人公的情感密度对心理时空引起的影响。举个例子来说，如果有一个观者都离故事主人公很近，即z0很小，但是因为这个观者是临时过来的，只是因为工作或者什么原因才临时过来待几天，这几天过去之后，该人物就会离去。这个观者的离去与那种朋友离去的情况完全不同，所以我们需要引入一个参数来描述每个人的重要程度，称之为弥散程度s。

解释清楚了这两个概念，那么如何用来这两个量来描述前面的心理弥散常数呢？我们定义这个量如下：

\[H(t)=-\frac 1 t \ln{s(1+z)}\]

做一个简单的变换，可以得到红移量、弥散系数以及conformal time的标度因子a之间的关系：

\[s(1+z)=\frac{1}{a}\]

为了便于理解，我们将会给出一张描述爱情的图表作为示例。

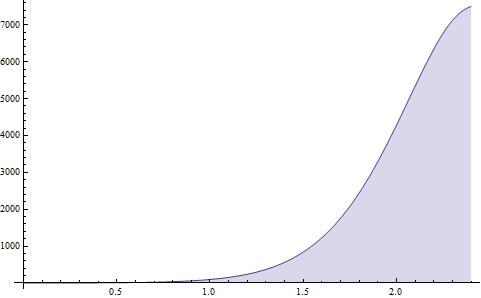
第二部分

从第一部分已经可以感觉到，实际上相对论的心理学至少能够描述一些我们日常生活中的一些心理现象。事实上要对这二个理论做一些澄清的最快的方法就是建立广相里面各种元素跟心理学里面的各种元素的对应。当然这不是唯一的路，我先试试，如果走不通在重新回到这里。{！我加一个breakpoint=1。}

在物理里面，我们描述某一个时空点发生了什么事件。而且我们希望有一个描述这个事件随时间的演化，而且一般我们希望这个描述是协变性的（这里我们要求广义协变）。

然而，在心理学里面要复杂的多。因为这是一个涉及到主观观测的理论。在物理学中，我们一般会寻找不会因为观测者的不同而便变化的物理量，或者说，我们一般的会有一个办法来严格的定义这些量，这样严格定义之后，物理量就可以被不同的主观观测者按照相同的方式来接受。在这个过程中，我们人为的排除掉了主观的影响。但是心理学偏偏就是要把主观感受的东西拖进理论中来。也就是说，我们下面的理论事实上需要给出一个从我们物理中所谓的客观事件到一个个体的主观感受之间的映射。

从数学上讲，只要我们能够给出了从客观实在的事件到主观感受之间的映射（我们非常希望这个是一个 $C^\infty$ 的微分同胚的映射，因为这样在操作映射的时候会变得简单的多），那么这个理论就算完成了。（还要看一下这些是不是可以放在微分流形上解决。或者条件放宽一点，我们只要求从客观M到主观的映射f是 $C^\infty$ 的。）当然，如果我们给出一个微分同胚的映射，那么由于物理规律的协变性，那么物理规律在通过微分同胚映射到了某个人的主观感受之后，规律必然也是协变的。

【注记1：这里关于这个映射是不是一个微分同胚的问题，讨论如下：考虑所有客观事件A可以在流行M上定义，引入M上的坐标系 $O_1$。该事件在个体的主观感受中的对应记作A′，我们可以很合理的定义从A到A′的映射f。这里假设了A只能在主观感受中产生一个对应。{！我在这里添加另一个breakpoint=2。}如果我们将要讨论的问题中，只考虑所讨论的体系中的所有主体都对一个客观事件有一个感受{A′}，那么这里就可以很合理的定义f的逆映射f−1，并且可以认为f和f′都是一一到上的映射。关于映射f和f−1的可微性的问题，我们可以这样考虑，即虽然我们可以找到很多这种映射，这些映射并不都是可微的，但是为了我们理论更简洁些，我们只能使用那些 $C^\infty$ 的映射。】

【注记2：在“该事件在个体的主观感受中的对应……”这句话中，出现了个体这个说法。实际上这个说法在以后的描述中会显得不那么恰当，因为个体这个概念已经不再那么重要。我们对这句话应该这样理解：我们会假定每个个体都不同，所以只需要给出每个个体的完整的主观感受集合就可以区分出个体。所以我们下面就采用这样的描述：“主观感受集合/流形M′中的对应……”】

当然，我们不仅仅要给出客观事件到主观客体的映射f，还有一个非常重要的问题是要给出这种主观感受从该个体到另一个个体的映射。数学上讲，这个可以通过一个pull back或者push forward来完成。可是，这里还有很多问题比如主观感受集合M′是不是流形？由于没有比较有说服力的推理，我们这里就假定这个问题的答案是肯定的吧。一种理解是，既然我们已经假定了这里用到的f和f′是可微的，M′和M就是非常像，考虑到我们在建立主观感受集合的时候，方法很多，类似于映射可微性的讨论，我们也是为了是的理论更简单，只挑出那部分可以构成流形的方法。

---