Monte Carlo Investigation of Frustrated Heisenberg Model
A simple vector model in 2 dimensions. Its Hamiltonian can be written as
\[H={ {J} { 1} }\sum\limits{i,j}{ { {s}{i} }{ {s}{j} } }+{ {J}{2} }\sum\limits{i’,j’}{ { { s}{i’} }{ {s}{j’} } },\]in which i,j means the nearest neighbor interaction when i’, j’ means the next nearest neighbor interaction. We designed the program under Honeycomb lattice, i.e.,
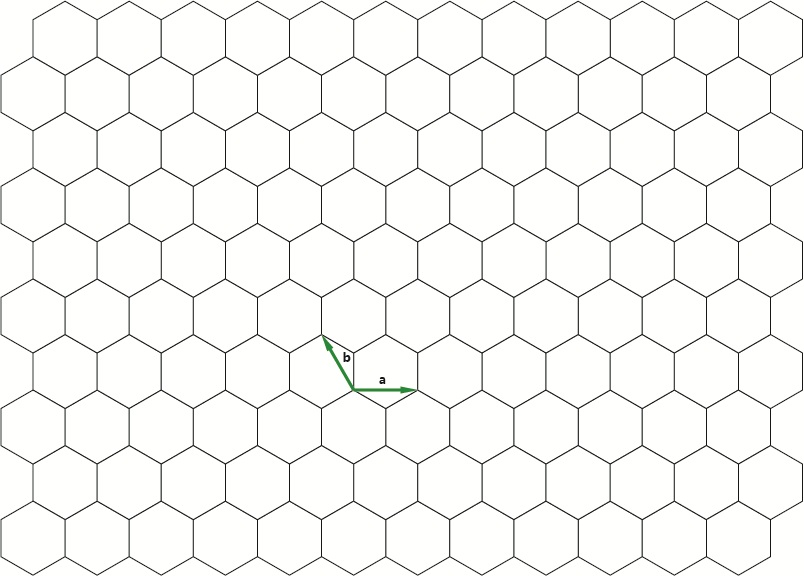
To make it clear for programming, we reshaped the lattice under homeomorphic:
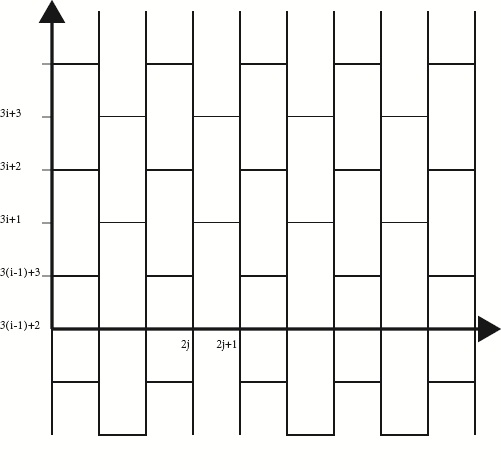
We wrote the Metropolis CODE with C:
/This program calculates the energy, heat capacity, magnetization, magnetic permitivity./
/Boundary condition: periodic boundary condition./
/In this program, J&k are put into T. To fill it to the expressions, just consider the dimensions./
include <stdio.h>
include <stdlib.h>
include <time.h>
include <math.h>
#define L 100
#define NGL 1000000 /*Samples Neglected*/
#define N_t 51000000 /*Total samples*/
#define N (N_t-NGL)
#define T_i 0.1
#define T_f 1.0
#define Tstep 0.1
#define SIZE_T 500 /*The size of emcx in T axis. Check this before compiling!*/
#define SIZE_R 60 /*The size of emcx in R axis. Check this before compiling!*/
#define R_i 50.0 /*Ration of J2/J1. Initial value.*/
#define R_step 0.1 /*step*/
#define R_f 50.0 /*End of R*/
#define Pi 3.1415926536
double sum_M[2]; /*sum_M[0] denotes the cos part; sum_M[1] denotes the sin part*/
double sum_Mag;
double s[L][L]; /*Size of the lattice*/
double sum_E;
double T;
struct Obsv
{
double C;
double X;
double M;
double E;
};
/********************************/
// FILE *fchk; //chk_sum_E
/********************************/
void Inist();
void Mag();
void Energy(double R);
void MCP(double R);
struct Obsv Cac_obsv(double R);
int main()
{
int i,j;
double R;
struct Obsv emcx[SIZE_T][SIZE_R];
FILE *ft,*fm,*fx,*fc,*fe,*fr;
fr=fopen("R.txt","w");
ft=fopen("T.txt","w");
fx=fopen("X.txt","w");
fc=fopen("C.txt","w");
fm=fopen("M.txt","w");
fe=fopen("E.txt","w");
/**********************************/
//fchk=fopen("Chk_dE.txt","w");
/**********************************/
R=R_i;
srand(time(NULL));
for(j=0;R< =R_f;j++)
{
T=T_i;
for(i=0;T<=T_f;i++)
{
Inist();
emcx[i][j]=Cac_obsv(R);
fprintf(fr,"%f\n",R);
fprintf(ft,"%f\n",T);
fprintf(fx,"%f\n",emcx[i][j].X);
fprintf(fc,"%f\n",emcx[i][j].C);
fprintf(fm,"%f\n",emcx[i][j].M);
fprintf(fe,"%f\n",emcx[i][j].E);
printf("-------------\n");
printf("R=%f\n",R);
printf("T=%f\n",T);
printf("X=%f\n",emcx[i][j].X);
printf("C=%f\n",emcx[i][j].C);
printf("M=%f\n",emcx[i][j].M);
printf("E=%f\n",emcx[i][j].E);
T = T+Tstep;
}
R+=R_step;
}
fclose(fr);
fclose(ft);
fclose(fx);
fclose(fc);
fclose(fm);
fclose(fe);
/*****************************/
//fclose(fchk);
/*****************************/
printf("The End!\n");
}
void Inist() /*Initialized lattice. All oriented to one direction*/
{
int i,j;
for(i=0;i {
for(j=0;j {
s[i][j]=0;
}
}
}
struct Obsv Cac_obsv(double R)
{
int i;
double E_avg=0.0;
double E_as=0.0;
double M_avg=0.0;
double M_as=0.0;
struct Obsv emcx;
Mag();
Energy(R);
for(i=0; i {
MCP(R);
/********************************/
//printf("chk.Cac_obsv.sum_Mag=%f\n",sum_Mag);
//printf("chk.Cac_obsv.sum_E=%f\n",sum_E);
//fprintf(fchk,"%f\n",sum_E);
/********************************/
if(i>=NGL)
{
E_avg+=(double)sum_E/N;
E_as+=(double)sum_E*sum_E/N;
M_avg+=(double)sum_Mag/N;
M_as+=(double)sum_Mag*sum_Mag/N;
}
}
emcx.E=E_avg;
emcx.M=M_avg;
emcx.C=(E_as - E_avg*E_avg)/T/T;
emcx.X=(M_as - M_avg*M_avg)/T;
return emcx;
}
/*Monte Carlo process.*/
void MCP(double R)
{
int i,j;
double agl_rdm;
double sum,sum_tmp,dE; /*sum_tmp is used to cal the energy difference*/
i=rand()%L;
j=rand()%L;
agl_rdm=(double)rand()/RAND_MAX*2*Pi; /*What if I just make it (double)rand()*/
/*Cal the energy before we add a random angle to s[i][j]*/
if(j%2==0)
{
if(i%2==0)
{
sum_tmp=cos(s[i][j]-s[i][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][j])+cos(s[i][j]-s[(i-1+L)%L][j]);
sum_tmp+=R*(cos(s[i][j]-s[(i+1)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+2)%L][j])+cos(s[i][j]-s[(i-2+L)%L][j]));
}
else if(i%2==1)
{
sum_tmp=cos(s[i][j]-s[i][(j+1)%L])+cos(s[i][j]-s[(i+1)%L][j])+cos(s[i][j]-s[(i-1+L)%L][j]);
sum_tmp+=R*(cos(s[i][j]-s[(i+1)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+2)%L][j])+cos(s[i][j]-s[(i-2+L)%L][j]));
}
}
else if(j%2==1)
{
if(i%2==1)
{
sum_tmp=cos(s[i][j]-s[i][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][j])+cos(s[i][j]-s[(i-1+L)%L][j]);
sum_tmp+=R*(cos(s[i][j]-s[(i+1)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+2)%L][j])+cos(s[i][j]-s[(i-2+L)%L][j]));
}
else if(i%2==0)
{
sum_tmp=cos(s[i][j]-s[i][(j+1)%L])+cos(s[i][j]-s[(i+1)%L][j])+cos(s[i][j]-s[(i-1+L)%L][j]);
sum_tmp+=R*(cos(s[i][j]-s[(i+1)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+2)%L][j])+cos(s[i][j]-s[(i-2+L)%L][j]));
}
}
else
{
printf("Checkpoint 1! j is neither odd nor even! Attention!");
}
/****************************/
//printf("chk.MCP.sum_tmp=%f\n",sum_tmp);
/****************************/
/*Add a random angle to s[i][j]*/
s[i][j]+=agl_rdm; /*Exceeding 2*Pi makes not sense in cos or sin func*/
/*Cal the energy after we add a random to s[i][j]*/
if(j%2==0)
{
if(i%2==0)
{
sum=cos(s[i][j]-s[i][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][j])+cos(s[i][j]-s[(i-1+L)%L][j]);
sum+=R*(cos(s[i][j]-s[(i+1)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+2)%L][j])+cos(s[i][j]-s[(i-2+L)%L][j]));
}
else if(i%2==1)
{
sum=cos(s[i][j]-s[i][(j+1)%L])+cos(s[i][j]-s[(i+1)%L][j])+cos(s[i][j]-s[(i-1+L)%L][j]);
sum+=R*(cos(s[i][j]-s[(i+1)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+2)%L][j])+cos(s[i][j]-s[(i-2+L)%L][j]));
}
}
else if(j%2==1)
{
if(i%2==1)
{
sum=cos(s[i][j]-s[i][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][j])+cos(s[i][j]-s[(i-1+L)%L][j]);
sum+=R*(cos(s[i][j]-s[(i+1)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+2)%L][j])+cos(s[i][j]-s[(i-2+L)%L][j]));
}
else if(i%2==0)
{
sum=cos(s[i][j]-s[i][(j+1)%L])+cos(s[i][j]-s[(i+1)%L][j])+cos(s[i][j]-s[(i-1+L)%L][j]);
sum+=R*(cos(s[i][j]-s[(i+1)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+1)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j+1)%L])+cos(s[i][j]-s[(i-1+L)%L][(j-1+L)%L])+cos(s[i][j]-s[(i+2)%L][j])+cos(s[i][j]-s[(i-2+L)%L][j]));
}
}
else
{
printf("Checkpoint 2! j is neither odd nor even! Attention!");
}
/********************************/
//printf("chk.MCP.sum=%f\n",sum);
/********************************/
dE=sum-sum_tmp; /*Attention!*/
/********************************/
//printf("chk.MCP.dE=%f\n",dE);
/********************************/
if(dE< =0)
{
sum_M[0]+=cos(s[i][j])-cos(s[i][j]-agl_rdm); /*Accept&Cal*/
sum_M[1]+=sin(s[i][j])-sin(s[i][j]-agl_rdm);
sum_Mag=sqrt(sum_M[0]*sum_M[0]+sum_M[1]*sum_M[1]);
sum_E+=dE;
}
else if(((double)rand()/RAND_MAX) {
sum_M[0]+=cos(s[i][j])-cos(s[i][j]-agl_rdm); /*Accept&Cal*/
sum_M[1]+=sin(s[i][j])-sin(s[i][j]-agl_rdm);
sum_Mag=sqrt(sum_M[0]*sum_M[0]+sum_M[1]*sum_M[1]);
sum_E+=dE;
}
else
{
s[i][j]=s[i][j]-agl_rdm; /*Reject the change*/
}
/********************************/
//printf("chk.MCP.sum_M[0]=%f\n",sum_M[0]);
//printf("chk.MCP.sum_M[1]=%f\n",sum_M[1]);
//printf("chk.MCP.cos(s[i][j])-cos(s[i][j]-agl_rdm)=%f\n",cos(s[i][j])-cos(s[i][j]-agl_rdm));
/********************************/
}
void Mag()
{
// int i,j;
// double dM_tmp[2]={0};
// for(i=0;i // {
// for(j=0;j // dM_tmp[0]+=cos(s[i][j]);
// dM_tmp[1]+=sin(s[i][j]);
// }
// sum_M[0]=dM_tmp[0];
// sum_M[1]=dM_tmp[1];
sum_M[0]=1.0*L*L;
sum_M[1]=0.0;
/********************************/
//printf("chk.Mag.sum_M[0]=%f\n",sum_M[0]);
//printf("chk.Mag.sum_M[1]=%f\n",sum_M[1]);
/********************************/
}
void Energy(double R)
{
// double dE_tmp;
// dE_tmp=(3.0+R*6.0)*L*L/2.0;
sum_E=(3.0+R*6.0)*L*L/2.0;
}