宇宙扰动的来源以及演化

在宇宙学中，原初扰动的问题一直是非常吸引人的话题。

起源

在很久很久之前，人们对于宇宙起初的那段时间的物理还不是很清楚，所以曾经有人猜测宇宙的原初扰动就是热扰动，$\delta=1/\sqrt{N}$，其中 $\delta=\delta\rho/\rho$，而 $\rho$ 是物质密度（此处先不讨论到底是什么的密度，可以理解为当时主导物质的密度），而N是粒子数。

但是后来Harrison（1970）发现，如果宇宙中的扰动起源于热涨落，那么我们会发现，这个涨落应该是在经典宇宙模型可以讨论的范围内的某个时刻突然出现的。这显然不合理，因为经典宇宙模型中没有什么机制会导致这样的结果。于是人们就只好做了假设，后来人们称之为Harrison-Zel’dovich Prescription。这个Prescription是说： All perturbations that come into the horizon have the same amplitude.

\[\Delta(k_i,t_i)=\Delta(k_e,t_e)=\text{Const.}\]

这里 $k=2\pi/L$ 是指comoving wavenumber.

Harrison可以通过一系列的argument把这个扰动的来源推到我们的经典的宇宙学模型不能讨论的地方。（Harrison, 1970）

后来，我们有了Inflation，通过一些列的讨论，可以让inflation产生合适的功率谱，

\[P_\Phi(k) = \frac{50\pi^2}{9k^3}\bigg( \frac{k}{H_0} \bigg)^{n-1}\delta_H^2\bigg( \frac{\Omega_m}{D_1(a=1)} \bigg)^2.\]

这个功率谱的好处，那么我们就可以通过如下定义得到一个无量纲的扰动量

\[\Delta^2(k)=\frac{k^3P(k)}{2\pi^2}.\]

如果我们看一下当今的 horizon crossing scale 的扰动，那么巧的很，$\Delta^2 = \delta_H^2$。为什么巧的很呢？因为这意味着，我们找到的这个无量纲的量，不仅仅是大小对于物质扰动的大小，而且在a=1的当今时刻，这个无量纲的量在horizon scale的值正好退化到物质扰动在horizon scale的值。这样非常有利于我们对于扰动的考察。

演化

其实所有的演化，都可以通过8个Boltzmann方程加上扰动的Einstein方程来解决。对于一些简单的情况，比如Dodelson(2008)中的只考虑0和1级的温度扰动极距的情况，可以使用仅仅5个简单的方程解决。

当然，就像通常那样，方程没有全时段的严格解，只能通过数值得到结果或者某些近似来得到简化的解析解。

举个例子吧。比如对于Super-horizon的情况，可以忽略所有k相关的项，并且使用一些合适的初始条件，可以得到如下的解,

\[\frac{\Phi(0)}{10}\frac{1}{x^3}(16\sqrt{1+x}+9x^3+2x^2-8x-16).\]

方程里面 $y=a/a_{equality}$ 。也就是scale factor与matter radiation equality的时候的scale factor的比值。

考虑y很大的情况，也就是a很大的情况，或者说是晚期的情况，$\Phi\sim 9/10 \Phi(0)$，也就是说，虽然是Super horizon的情况，但是晚期的引力势强度还是有所减弱。从方程上来看，这个是情理之中，因为即使是Super horizon的，依然是跟scale factor相关的，或者说跟dark matter的比例相关的。

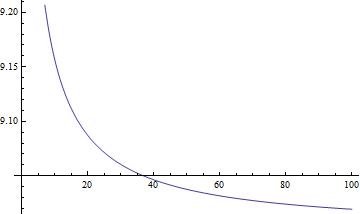
图中没有显示出早期的扰动的情况，因为我随手把前面的系数设定了一下，这种情况下，mathematica只能算到大约y∼0.0003以后的情况，再往前算，直接plot命令就不准确了。事实上，早期的扰动，或者说在早期远离matter radiation equality的时候，扰动势应该是常数。Dodelson的Modern Cosmology里面第七章的Figure 7.6就给出了理论和数值的对照。

同样，我们也可以通过舍弃掉物质的影响，来考虑远远早于matter radiation equality时期进入到视界的扰动，最终我们得到的势函数的图像类似下面这种图：

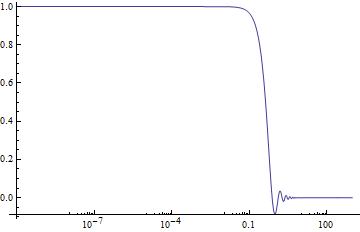
早期是常数，这跟我们的假定不谋而合。后来在radiation domination后期快速衰减振荡，最初变为常数。