Finite Difference Discretization
Algorithms for Solving The Advection-Diffusion Equation
前面我们获得了体系的方程,下面我们看看如何来用计算机解决问题。
\begin{eqnarray}
\omega_t + [\psi, \omega] &=& v\nabla^2 \omega
\nabla^2 \psi &=& \omega
\end{eqnarray}
体系的范围: \(x, y \in [-L, L]\)
初始条件: \(\omega(x,y,t=0)=\omega_0\)
周期性边界条件:
\begin{eqnarray}
\omega(-L, y, t) &=& \omega(L,y,t)
\omega(x,-L,t) &=& \omega(x,L,t)
\end{eqnarray}
重新整理方程, \(\omega_t = v \cdot \nabla^2 \omega - [\psi, \omega]\)
利用 Taylor 展开 \(\frac{\omega_{n+1} - \omega_n}{ \Delta t } = v\cdot \nabla^2 \omega_n - [\psi_n,\omega_n]\) 即 \(\omega_{n+1} = \omega_n + \Delta t [ v\cdot \nabla^2 \omega_n - [ \psi_n,\omega_n ] ]\)
下面的操作步骤:
- 计算初始的 stream function $\psi$: $\nabla^2 \psi = \omega$
- 计算下一步,即 $\Delta t$ 之后的
- 重复上面的步骤
如何计算 $\psi_n$ 呢?我们有方程 $\psi_{xx} + \psi_{yy} = \omega$,而 $\omega$ 是可以通过上面的一阶的 Taylor 展开方程计算的。
我们需要借助之前的离散话的方法。把整个体系所在的 x y 平面网格化:
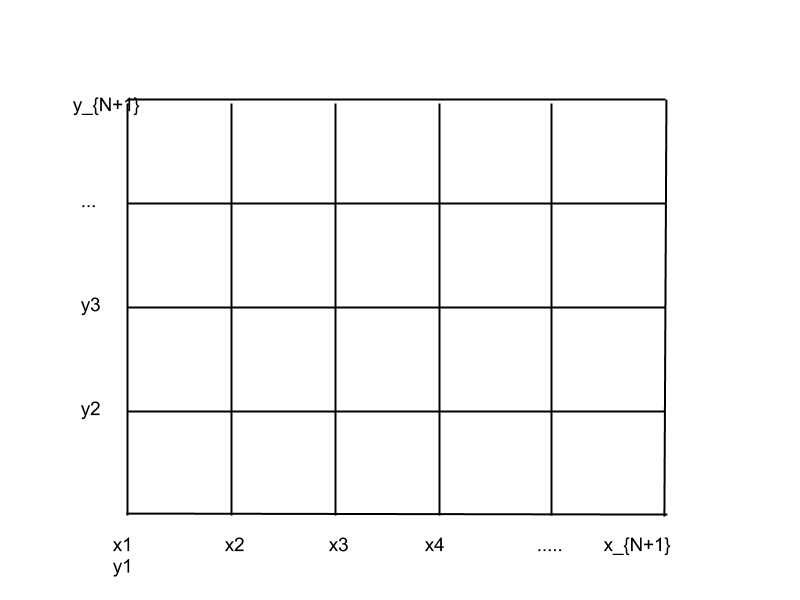
定义这样的量 \(\psi_{mn} = \psi(x_m,y_n)\)
那么周期边界条件可以写成
\begin{eqnarray}
\psi_{1j}&=&\psi_{N+1,j}
\psi_{i1}&=&\psi_{i,N+1}
\end{eqnarray}
写成这样之后,$\psi_{mn}$ 的二阶导数的计算方法
\begin{eqnarray}
(\psi_{mn}){xx} &=& \frac{ \psi{m+1,n} - 2\psi_{mn} + \psi_{m-1,n} }{\Delta x^2}
(\psi_{mn}){yy} &=& \frac{ \psi{m,n+1} - \2\psi_{mn} + \psi_{m,n-1} }{\Delta y^2}
\end{eqnarray}
进而我们得到 $\omega_{mn}$ 的导数的表达式
\[\delta^2 \omega_{mn} = -4 \psi_{mn} + \psi_{m+1,n} + \psi_{m-1,n} +\psi_{m,n+1} + \psi_{m,n-1}\]这样我们就可以写成 $\bf A \cdot \bf x = \bf b$ 的形式了。当然这里 $\bf x$ 是 $\psi$ 的离散化。