Euler, Runge-Kutta and Adams Methods

Euler 方法

\[y_{n+1} = y_n + \Delta t f(t_n, y_n)\]

利用目前的 y 和斜率来预测下一步的 y。

推广：

\[y(t+\Delta t) = y(t) + \Delta t [ A f(t,y(t)) + B f(t+P \Delta t, y + Q \Delta t f(t, y)) ]\]

即，我们可以对 Euler 方法进行高阶修正。为什么这么说？我们可以分别对上式的左边和右边进行 Taylor 展开，然后对照，发现 P,Q 与 $\Delta t$ 的高阶项的系数有关。 用同样的方法，可以得出 A, B, P, Q 之间的关系（当保留二阶无穷小的时候）。

\[A+B=1 \\ A P=1/2 \\ B Q=1/2\]

推导过程中可以注意到，P，Q 只会影响到三阶无穷小。

而且如果我们在推导中，只保留更低阶的无穷小（一阶无穷小），就回到 Euler 方法了。

Heun’s method

$A=1/2$ 时，对应的是 Heun’s method.

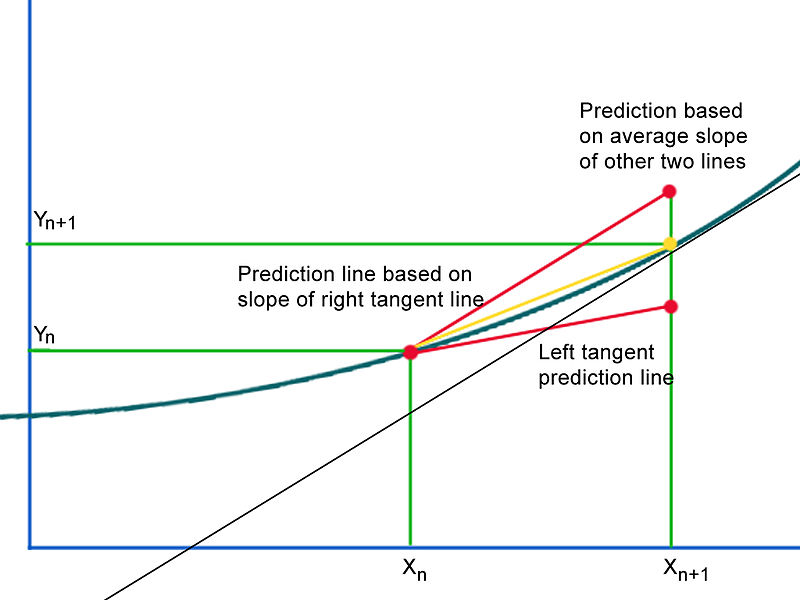
这种方法正好是取了 $y_n$ 点的和 $y_{n+1}$ 两点的切线做了平均来预测下一步的函数值的。

二阶 Runge-Kutta 方法

二阶的 RK 方法，要求

A=0

这种方法是取了中点的。

四阶的 RK

\[y_{n+1} = y_n + \frac{\Delta t}{6} ( f_1 + 2f_2 + 2f_3 + f_4 ) + O(\Delta t^5)\]

太精确了。

Integral and Anam’s Mehtod

积分有没有用呢？

利用积分，将我们要解决的问题

\[\frac{\mathrm dy}{\mathrm dt} = f(t,y)\]

写成

\[y_{n+1} = y_n + \int_{t_n}^{t_{n+1}} f(t,y) \mathrm dt\]

但是，问题在于，我们并不知道右侧的那个积分是如何解的，因为只有我们知道了 y 的精确形式，才能解这个积分。

在计算中，我们的方法是

\[y_{n+1} \approx y_n + \int_{t_n}^{t_{n+1}} p(t,y)\mathrm dt\]

$p(t,y)$ 是 $f(t,y)$ 的多项式的近似。

这是很合理的，因为 $[t_n, t_{n+1}]$ 是一段很小的间隔，所以 $f(t,y)$ 的变化不大，可以用多项式来近似。

Adams Time-Stepping Schemes

从上一节，我们了解到 Adam’s 方法实际上就是利用了积分，并且采用多项式来代替 y 的斜率。具体说来，Adam’s 方法根据所使用的多项式是否包含过去、现在、未来的点，有以下几种。

Adams-Bashforth

最简单的可以用来对 f(t,y) 做近似的多项式是常数，所以我们来试试常数。

\[p_1(t,y)=\text{Constant} = f(t_n,y_n)\]

把这个形式代入

\[y_{n+1} = y_n + \int_{t_n}^{t_{n+1}} p_1(t,y)\mathrm dt\]

中，

\[y_{n+1} \approx y_n + \Delta t f(t_n,y_n)\]

这正好回到了 Euler 方法。

如果我们用 \(p_2(t,y) = f_n + \frac{f_n - f_{n-1}}{2}(t-t_{n-1})\) 即考虑斜率的影响。

得到

\[y_{n+1} = y_n + \frac{\Delta t}{2} [ 3f(t_n, y_n) - f(t_{n-1},y_{n-1}) ]\]

Adams Moulton

可以用未来、现在、过去的点来计算未来的点。

\[p(t,y) = \text{Constant} = f(t_{n+1}, y_{n+1})\]

我们得到

\[y_{n+1} = y_n + \Delta f(t_{n+1}, y_{n+1})\]

可是 $ f(t_{n+1}, y_{n+1}) $ 是未知的，一种做法是用其它的方法先获得一个未来的点，例如用 Euler 法来算出一个未来的点，再把这个点代入到这种方法中。

为什么要多次一举呢？因为这种方法的稳定性很棒。