Boundary Value Problems: Direct Solve and Relaxation
这一节我们将会学习到使用离散化的方法:Discretization .
Computing Derivatives with Taylor Series
课堂笔记:
边值问题: \(\frac{\mathrm d^2 y}{\mathrm d t^2} = f(t,y,\frac{\mathrm d y}{\mathrm dt})\)
\begin{eqnarray}
\alpha_1 y(a) + \beta_1 \frac{\mathrm dy(a)}{\mathrm dt}&=&\gamma_1 \
\alpha_2 y(a) + \beta_2 \frac{\mathrm dy(a)}{\mathrm dt}&=&\gamma_2
\end{eqnarray}
现在我们考虑一个简单些的例子:
\(\frac{\mathrm d^2 y}{\mathrm dt^2} = f(y,\frac{\mathrm dy}{\mathrm dt},t)\)
边界条件是:
\begin{eqnarray}
y(a)&=&\alpha
y(b)&=&\beta
\end{eqnarray}
我们不喜欢这里面的导数,想要去掉里面的一阶导数和二阶导数。从而把这些变成线性方程组。
我们之前一直用到 Taylor 展开的方法。现在我们再用一次。
\begin{eqnarray}
f(t+\Delta t) &=& f(t) + \Delta t \frac{\mathrm d f}{\mathrm dt} + \frac{1}{2}\Delta t^2 \frac{\mathrm d^2 f}{\mathrm dt^2} + \frac{1}{3!}\Delta t^3 \frac{\mathrm d^3 f(c_1)}{\mathrm dt^3}
f(t - \Delta t) &=& f(t) - \Delta t \frac{\mathrm d f}{\mathrm dt} + \frac{1}{2}\Delta t^2 \frac{\mathrm d^2 f}{\mathrm dt^2} - \frac{1}{3!}\Delta t^3 \frac{\mathrm d^3 f(c_2)}{\mathrm dt^3}
\end{eqnarray}
然后我们把两个式子相减: \(f(t + \Delta t) - f(t-\Delta t) = 2 \Delta t \frac{\mathrm df}{\mathrm dt} + \frac{1}{3!}\Delta t^3 \left( \frac{\mathrm d^3 f(c_1)}{\mathrm dt^3} + \frac{\mathrm d^3 f(c_2)}{\mathrm dt^3} \right)\)
我们的目的是要把 $\frac{\mathrm df}{\mathrm dt}$ 表示出来,以便放进原来的方程中的导数都去掉,所以变形一下:
\[\frac{\mathrm df}{\mathrm dt} = \frac{f(t + \Delta t) - f(t-\Delta t)}{2\Delta } - \frac{1}{2}\frac{1}{3!} \Delta t^2 \frac{\mathrm d^3 f(c)}{\mathrm dt^3}\]然后,上面是精确的表达式,我们不知道 c 是什么,所以打算扔到这个二阶小量,即 \(- \frac{1}{2}\frac{1}{3!} \Delta t^2 \frac{\mathrm d^3 f(c)}{\mathrm dt^3} = O(\Delta t^2)\) 要扔掉。
这部分实际上就是用了最近邻的两个点来对要计算的点的切线做近似,如下图所示。

Second Order Derivatives and Forward and Backward Differences
上面我们把两个 Taylor 展开相减,消去了 $\Delta t$ 的偶数次幂的项,现在我们如果把两个式子相加,就能得到二阶导数的表达式:
\[f’’(t) = \frac{f(t+\Delta t) -2f(t) + f(t-\Delta t) }{ \Delta t^2 } + O(\Delta t^2)\]看看我们对于导数的处理,可以发现实际上我们只利用了要每个点的最近邻的两个临近的点来计算的:要计算蓝色的点,需要考虑两个橘色的点。

Boundary Value Problems and Ax=b
MATLAB 是设计用来解决线性代数问题 $\mathbf A \mathbf x = \mathbf b$ 的,所以我们希望我们的离散化的方法解决问题的时候,可以化成上面这种线性的形式。
首先把我们的问题完整的写出来(把我们之前离散化的导数带回到最初的问题中,并合并同类项,就得到一个递推公式)
\[\frac{1}{2}(1-p(t) \Delta t) y(t+\Delta t) + (-2 - \Delta t^2 q(t) ) y(t) + ( 1+ \frac{1}{2} p(t) \Delta t ) y(t-\Delta t) = r(t) \Delta t^2\]这样,我们就能写出矩阵形式了。
首先,我们对离散化的量标号: $y(a) = y_0$ $y(a+\Delta t) = y_1$ $y(a + 2 \Delta t ) = y_2$ … $y(b) = y_{N+1}$
$p(a) = p_0 $p(a+\Delta t) = p_1$ $p(a+2\Delta t) = p_2$ … $p(b) = p_{N+1}$
同样的方式对 $q(t)$ 编号。
然后,我们写出前几个式子看看:
\begin{eqnarray}
y_2 ( 1- \frac 1 2 \Delta t p_1 ) + y_1 (-2 - q_1 \Delta t^2) + y_0 (1 + \frac 1 2 p_1 \Delta t) &=& r_1 \Delta t^2
y_3 ( 1- \frac 1 2 \Delta t p_2 ) + y_2 (-2 - q_2 \Delta t^2) + y_1 (1 + \frac 1 2 p_2 \Delta t) &=& r_2 \Delta t^2
\cdots &&
y_{N+1} ( 1- \frac 1 2 \Delta t p_N ) + y_N (-2 - q_N \Delta t^2) + y_{N-1} (1 + \frac 1 2 p_N \Delta t) &=& r_N \Delta t^2
\end{eqnarray}
我们要写成这样的形式: \(\mathbf A \cdot \mathbf x = \mathbf b\)
当然,这里的 \(\mathbf x = \begin{pmatrix} y_1 \\ y_2 \\ \cdot \\ \cdot \\ \cdot \\ y_N \end{pmatrix}\)
根据我们写出来的几个例子,我们猜测 $\mathbf A$ 大致应该是
\[\mathbf A = \begin{pmatrix} (-2-q_1 \Delta t^2) & (1-\frac 1 2 p_1 \Delta t) & 0 & 0 & 0 \\ (1+\frac 1 2 p_1 \Delta t) & (-2-q_2 \Delta t^2) & (1-\frac 1 2 p_1 \Delta t) & 0 & 0 \\ & \cdot & & & \\ & & \cdot & & \\ & & & \cdot & \\ 0 & 0 & 0 & (1+\frac 1 2 p_N \Delta t) & y_N \end{pmatrix}\]对于右侧的 $\mathbf b$,我们猜测大致应该是
\[\mathbf b = \begin{pmatrix} r_1 \\ y_2 \\ \cdot \\ \cdot \\ \cdot \\ y_N \end{pmatrix}\]Boundary Implementation
但是,我们再看看第一个和最后一个式子:
\begin{eqnarray}
y_2 ( 1- \frac 1 2 \Delta t p_1 ) + y_1 (-2 - q_1 \Delta t^2) + y_0 (1 + \frac 1 2 p_1 \Delta t) &=& r_1 \Delta t^2
y_{N+1} ( 1- \frac 1 2 \Delta t p_N ) + y_N (-2 - q_N \Delta t^2) + y_{N-1} (1 + \frac 1 2 p_N \Delta t) &=& r_N \Delta t^2
\end{eqnarray}
我们写成矩阵之后,$y_0$ 和 $y_{N+1}$ 呢?看来看去,怎么也放不进 $\mathbf A$ 中了。那么怎么办呢?
我们把第一个和最后一个式子变形:
\begin{eqnarray}
y_2 ( 1- \frac 1 2 \Delta t p_1 ) + y_1 (-2 - q_1 \Delta t^2) &=& r_1 \Delta t^2 - + y_0 (1 + \frac 1 2 p_1 \Delta t)
y_N (-2 - q_N \Delta t^2) + y_{N-1} (1 + \frac 1 2 p_N \Delta t) &=& r_N \Delta t^2 - y_{N+1} ( 1- \frac 1 2 \Delta t p_N )
\end{eqnarray}
这样我们可以通过仅仅修改右侧的 $\mathbf b$ 为
\[\mathbf b = \begin{pmatrix} r_1 \Delta t^2 - + y_0 (1 + \frac 1 2 p_1 \Delta t) \\ y_2 \\ \cdot \\ \cdot \\ \cdot \\ r_N \Delta t^2 - y_{N+1} ( 1- \frac 1 2 \Delta t p_N ) \end{pmatrix}\]来得到正确的 $\mathbf A \cdot \mathbf x = \mathbf b$.
Nonlinear Boundary Value Problems
有时候问题并不是上面我们解决的问题那么简单,$y’’ = f(t,y,y’)$ 中的 $f(t,y,y’)$ 可能是一个很复杂的形式。
我们做初步的处理的话,
\[\frac{ y_{n+1} - 2y_n + y_{n-1} }{ \Delta t^2 } = f(t,y_n, \frac{y_{n+1} - y_{n-1} }{ 2\Delta t })\]如果右侧的形式特别复杂,我们所能做的最好事情是给出一个很好的用于启动的猜测。非线性问题很大程度有依赖于这种猜测。
可以用一个 Newton 法的例子看看为什么一个好的初始猜测很重要。Newton 切线法中,我们要找到方程 $f(x)=0$ 的解。方法是先随便在一个我们认为很接近解的地方开始,例如从 $x_1$ 开始,找出$(x_1, f(x_1))$ 点的切线,然后切线会与 x 轴相交,例如交点是 $(x_2,0)$,我们再从 $(x_2,f(x_2))$ 开始重复这个过程,直到最后,我们会越来越接近我们的真实的 $f(x)=0$ 的解。过程如下:
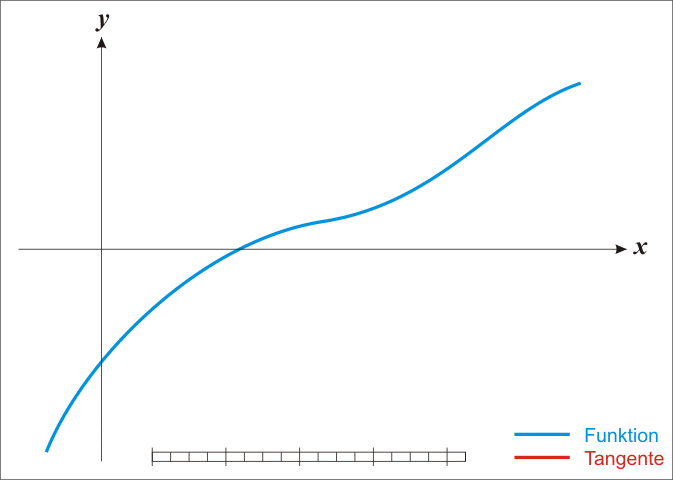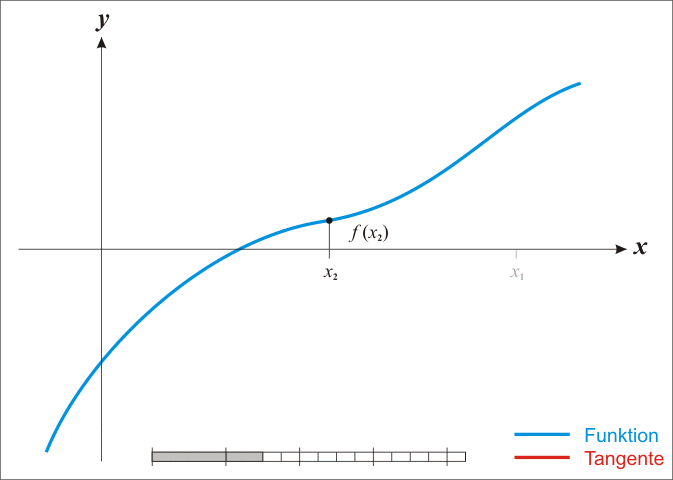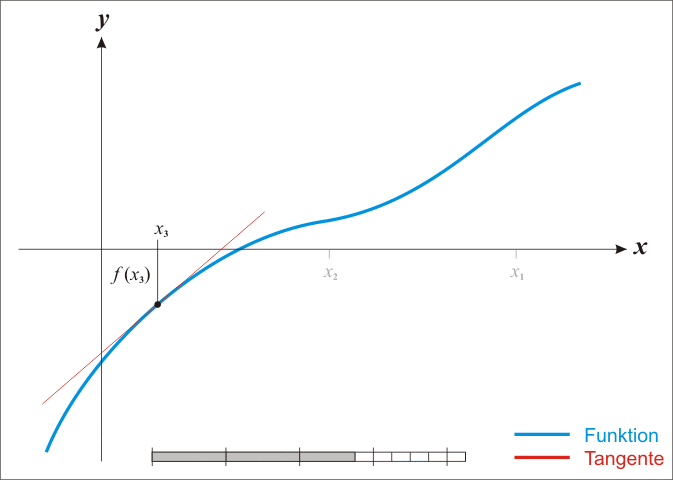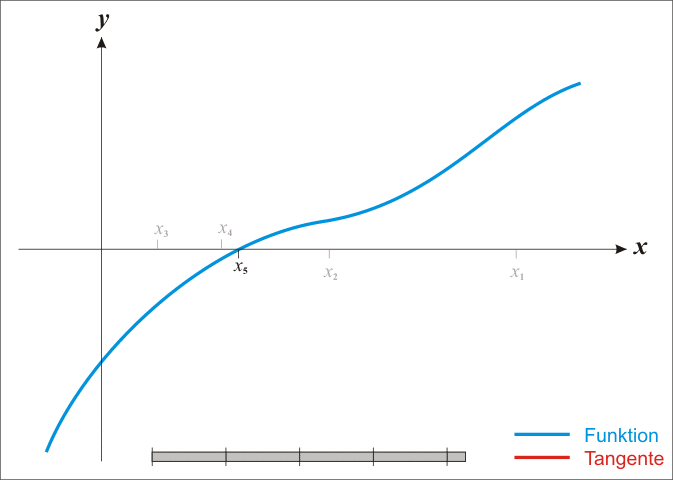
这个过程中,我们充分利用了计算机的优势:善于做那种固定路子的重复性的工作,例如循环。