A Basic Jacobi Iteration Procedure
回顾
我们要解决的问题是
\[\mathbf A x = b\]为什么要解决这个问题呢?因为我们可以把一些问题转换成这类线性问题,例如我们可以把 $\nabla^2 \psi = \omega$ 通过离散化等方法来转换成上面的矩阵方程。
总结我们之前学过的方法,共有
- Euler
- RK
- Adams
- Shooting method
- Finite difference discretization
然后离散化之后,我们需要解决$\mathbf A x = b$的问题,然后我们已经有了下面的方法
- Gaussian Elimination
- LU Decomposition
然后我们下面要学的是
- Jacobi Iteration
- Gauss-Seidel
两种。
Jacobi Iteration
我们来看一个例子:
\[\begin{eqnarray} 4x-y+z=7\\ 4x-8y+z=-21 \\ -2x + y + 5z = 15 \end{eqnarray}\]我们可以对这些式子变形:
\[\begin{eqnarray} x=\frac{7+y-z}{4} \\ y=\frac{21+4x+z}{8} \\ z=\frac{15 + 2x -y}{5} \end{eqnarray}\]Done! 我们已经解出来啦。
等等,这些解里面有未知数啊?没问题,我们可以这样做。
- 首先猜测一组 x, y, z 的解
- 把这组解代入右边获得新的一组解
- 把新的解代入右边再获得新的解
这样不断迭代,就可以得到最终的解了。
我绘制了这个例子中,进行十次迭代的过程。横轴表示迭代的次数,纵轴表示x,y, z 的结果。
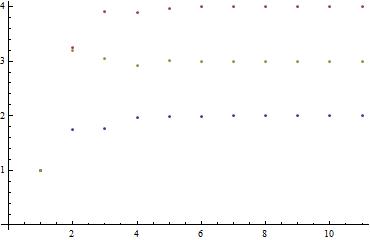
对于的列表是
\{\{1, 1.75, 1.7625, 1.9625, 1.99062, 1.99109, 1.99859, 1.99965, 1.99967, 1.99995, 1.99999\}, \{1, 3.25, 3.9, 3.8875, 3.97188, 3.99625, 3.99578, 3.99895, 3.99986, 3.99984, 3.99996\}, \{1, 3.2, 3.05, 2.925, 3.0075, 3.00188, 2.99719, 3.00028, 3.00007, 2.99989, 3.00001\}\}
在多次迭代之后,三个解都收敛了。实际上这三个收敛的结果就是x,y,z对于的解,即2,3,3。
收敛性
在高兴之余,我们可以考虑这样一种情况,即我们把三个方程的顺序换一下。
然后我们发现有的情况迭代的结果居然不收敛了。
这是为什么呢?这是因为 Jacobi Iteration 需要方程满足 SDD, Strict diagonal dominace 条件:
如果 $\vert a_{kk} \vert > \sum\limits_{j=1,j\neq k} \vert a_{kj} \vert$,那么我们就说这个矩阵是 SDD 的。
如果一个矩阵是 SDD 的,那么可以确保 Jacobi Iteration 的方法得到的结果是收敛的,不管初始的猜测有多坏。
$O(N\cdot K\cdot ?)$
K 是迭代的次数,N 是维数。另外这个还跟矩阵里面与多少相邻的有关。
更快的方法
我们上面的方法把迭代式子写出来,是
\[\begin{eqnarray} x_{K+1} = \frac{7 + y_K -z_K }{ 4 } \\ y_{K+1} = \frac{21 + 4 x_K + z_K }{ 8 } \\ z_{K+1} = \frac{15 + 2 x_K - y_K }{ 5 } \end{eqnarray}\]但是,我们返回来想想,我们为什么不立刻就使用我们已经得到的 $x_{K+1}$ 呢?这样会更快么?大致是更快的。
总结
解线性方程的方法
- Gaussian Elimination
- LU Decomposition
- Jacobi Iteration
- Gauss-Seidel