展开和变换
预备工作:
In[191]:=
![]()
数项级数
情形一
我们常常使用级数。那么级数如何形象的去理解呢?
举个例子说明,比如我们有一个这样的数列:
![]()
我们可以把这些数画在一个坐标系中。例如我们有这样一个数列:
In[192]:=
![]()
数列的前几项是:
In[193]:=
![]()
Out[193]=
![]()
我们可以把各项在图上表示出来。其中
In[194]:=

Out[195]=
 |
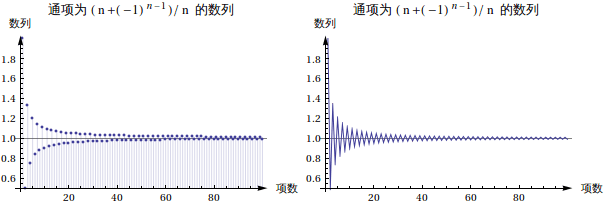 |
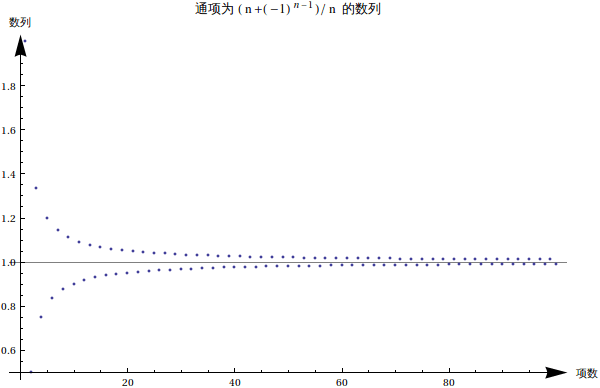
从这个图中看到这个数列的极限通项大概是越来越接近 1 的。那么它的极限到底是不是 1 呢?
In[196]:=
![]()
Out[196]=
![]()
确实是 1 。
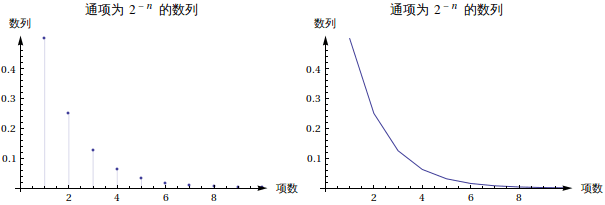
情形二
另一种情形是这样的。
In[197]:=
![]()
In[198]:=
![]()
Out[198]=
![]()
In[199]:=

Out[200]=
 |
 |
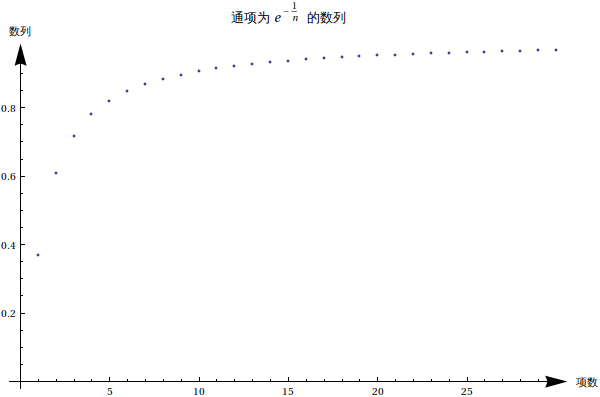
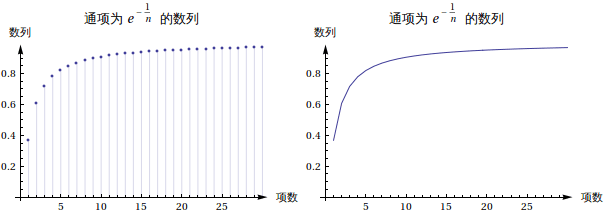
情形三
In[201]:=
![]()
In[202]:=
![]()
Out[202]=
![]()
In[203]:=

Out[204]=
 |
 |
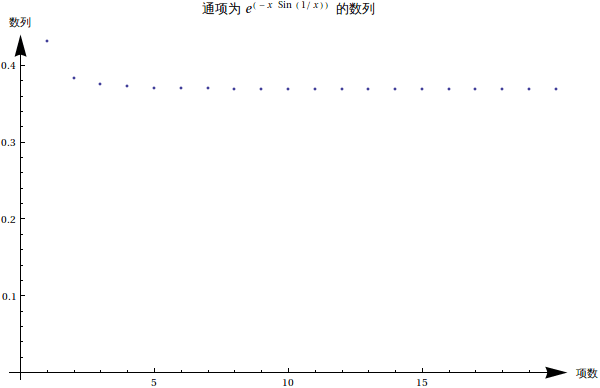
情形四
In[205]:=
![]()
In[206]:=
![]()
Out[206]=

In[207]:=

Out[208]=
 |
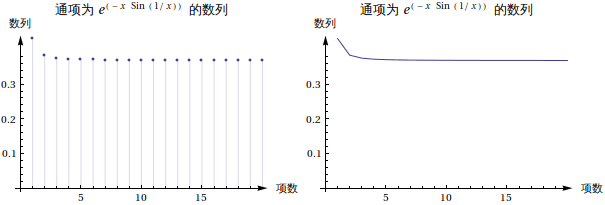 |
In[209]:=
![]()
Out[209]=
![]()
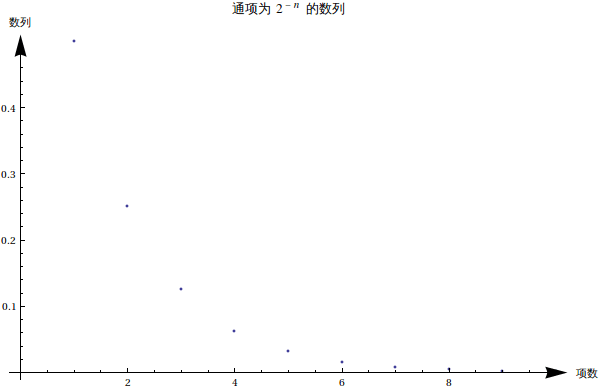
有一点要很小心,即这个数量通项写出来虽然是一个递减的,然而这个通项所对应的连续自变量的函数却是个振荡的。
In[210]:=
![]()
Out[210]=
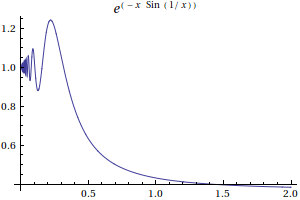
这是一个有警示性的例子。有时候我们找了几个自变量,算了函数值,然后我们就武断的给出了函数是个单调性等性质,看看这个例子的情况,我们就知道有时候是必须很小心的。
其他情形
当然还用其他的情形。比如函数一直保持在某值下方,但是却震荡着接近该值等等。还用趋于无穷的各种情况。
数项级数收敛
级数是否收敛,需要判断级数和随项数的变化趋势。我们有各种准则来判断,不过我们这里不是来讨论准则的,而是来看图的。
关于收敛的简单例子
调和级数是一个很经典的级数。
In[211]:=
![]()
Out[211]=
![]()
In[212]:=
![]()
Out[212]=
![]()
In[213]:=

Out[213]=
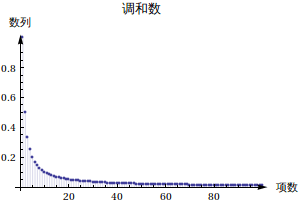 |
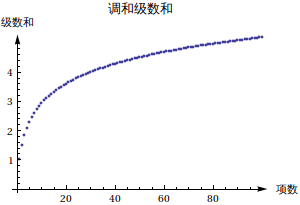 |
继续往后画,可以发现级数和依然没有停止增长的趋势,实际上调和级数是发散的:
In[214]:=
![]()
Out[214]=
![]()
上面在画调和级数的图像的时候,我为什么要把线条下面加竖线阴影呢?级数和是什么意思?就是我所画的这些数值的线段的长度加起来。或者,一个更好的理解方法是,我们把左边的那个画成 BarChart,如下图
In[215]:=
![]()
Out[215]=
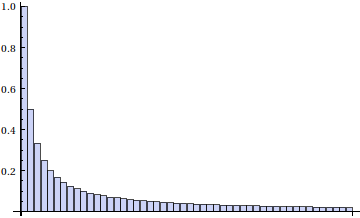
我们可以认为级数和就是这些竖条的面积,因为这些竖条的宽都是 1 。也就是说,虽然随着 n 增大,每项的值越来越小,但是还是减小的不够快(看上面调和级数和的图和级数和极限的结果)。
我们稍微改动一下,把原来通项的分母上的 n 换成 n^2 。这样我们再看看。
In[216]:=
![]()
Out[216]=
![]()
In[217]:=

Out[217]=
 |
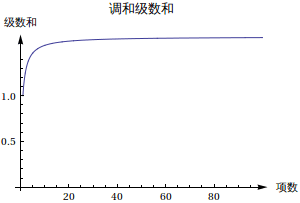 |
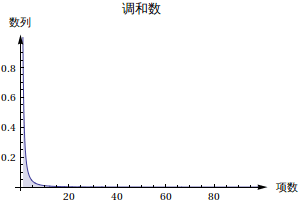
改过之后的级数随着项数的增加减小的更快了。从右侧的级数和的情况来看,有希望是一个收敛的。我们来验证一下:
In[218]:=
![]()
Out[218]=
![]()
果然是收敛的。也就是说当我们让第一个调和级数减小速度的更快之后,有可能获得一个收敛的级数。
这两个例子也告诉我们,虽然调和级数只看左边的级数分布的图似乎是与横轴所夹面积是收敛的(毕竟单调减少嘛),但是我们不能看看这个图就下结论,而且实际上上面证明我们的感觉是错的。所以我们需要一些定理一些准则来帮助我们做收敛判断。
条件收敛的例子
如果我们的级数 An 是收敛的,但是 |An| 级数却不收敛,那么我们就说这是条件收敛。
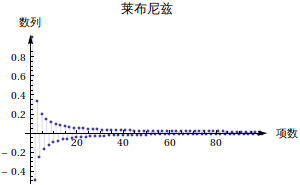
我们拿莱布尼兹级数来做例子。各个项为:
In[219]:=
![]()
Out[219]=
![]()
级数为
In[220]:=
![]()
Out[220]=
![]()
In[221]:=

Out[221]=
 |
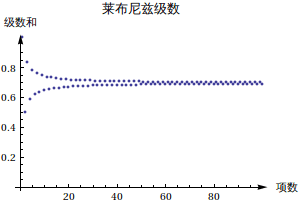 |
看起来是收敛的,我们证明一下:
In[222]:=
![]()
Out[222]=
![]()
确实是收敛的。
而莱布尼兹级数如果每项加绝对值,就变成了调和级数,我们前面证明了调和级数不收敛。所以莱布尼兹级数其实是条件收敛的。
函数级数
除了数项级数,我们还有函数级数。函数级数是一个很重要的概念,因为这会涉及到我们后面很多的内容。
一个简单的函数级数的项的例子是:
In[223]:=
![]()
Out[223]=
![]()
相应的级数(和)是:
In[224]:=
![]()
Out[224]=
![]()
In[225]:=
![]()
Out[225]=
![]()
In[226]:=

Out[226]=
 |
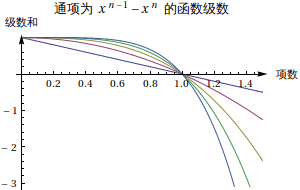 |
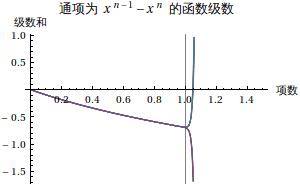
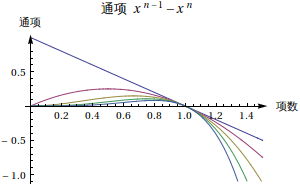
左边是各个通项,随着 n 的增加,通项函数值越来越小;右边是级数的情况,随着 n 的增加,级数在 (0,1) 部分都是限制在 1 以下的,但是在 (1,Infinity) 范围内看起来却没有下限。
我们来验证上面的直观印象:
In[227]:=
![]()
Out[227]=
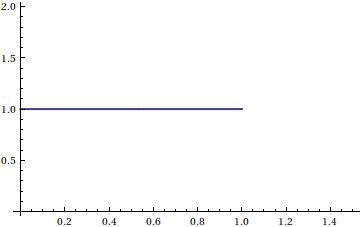
在上面的线段的端点上看不出来,我们单独给个数字:
在 x=1 点:
In[228]:=
![]()
Out[228]=
![]()
在 x=0 点:
In[229]:=
![]()
Out[229]=
![]()
为什么 x>1 的部分没有显示?我们釆点看看。取 x 为 {1.1,1.2,1.3,1.4,1.5,1.6}几个点:
In[230]:=
![]()
Out[230]=
![]()
有种很重要的幂级数是幂级数。我们前面看了莱布尼兹级数,就是以 1/n x^n 幂级数的一种特殊情况(x=-1)
这个特殊的幂级数通项:
In[231]:=
![]()
Out[231]=
![]()
明显当 x=-1 时就变成莱布尼兹级数通项了。
幂级数里面有个阿贝尔定理,说的是如果幂级数在 x=r>0 时收敛,那么幂级数在区间 [0,r] 上一致收敛。我们通过例子来形象的看看这个定理。通项:
In[232]:=
![]()
Out[232]=
![]()
级数和
In[233]:=
![]()
Out[233]=
![]()
这个级数在 x=1 时的极限:
In[234]:=
![]()
Out[234]=
![]()
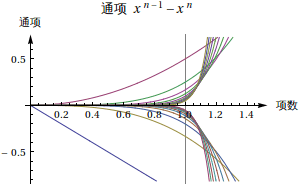
那么按照阿贝尔定理,我们的这个幂级数在 [0,1] 上一致收敛的。
In[235]:=

Out[235]=
 |
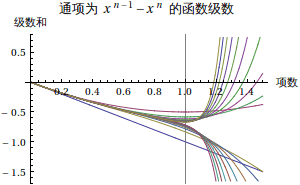 |
看起来是在 (0,1) 收敛的。这个级数和在 0<=x<=1 时是递增的,如果在 x=1 处收敛,那么在 [0,1] 上也是收敛的,而且是一致收敛(需证明,直观的请看下图,绘制了 100 项到 109 项。)。
In[236]:=
![]()
Out[236]=