Today I Learned
Sum of Squares and Torque
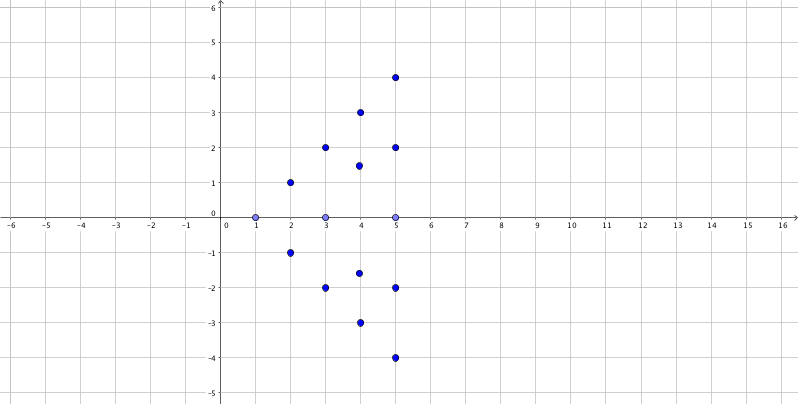
Suppose we have the mass of each dot on the coordinate system as $m$, the overall torque due to gravity is
\[\begin{align} \tau_5 &= mg\cdot d + 2 mg \cdot 2 d + 3 mg \cdot 3 d + \cdots + 5 mg \cdot 5 d \\ & = m g \cdot d \left( 1^2 + 2^2 + 3^3 +\cdots + 5^2 \right). \end{align}\]This can be generalized to arbitary $n$,
\[\begin{align} \tau_n &= mg \cdot d \left( 1^2 + 2^2 + 3^2 + \cdots + n^2 \right) \\ & = mg\cdot d \sum_{i=1} i^2. \end{align}\]On the other hand the total torque of the system is simply the displacement of center of gravity cross total gravitational force.
The center of the gravity is at $2/3$ on the line that is perpendicular to the base of the isosceles triangle, which is
\[\left( \frac{2}{3} (n-1) + 1 \right) d,\]where the $1$ is because the top of the triangle is at coordinate 1.
The value of total gravitational force is the sum is
\[\sum_{i=1}^n i\cdot mg = mg \sum_{i=1}^n i\]Now the torque due to gravity is
\[\begin{align} \tau_n &= d \left( \frac{2}{3} (n-1) + 1 \right) \left( \sum_{i=1}^n i\cdot mg \right) \\ & = mg\cdot d \frac{2n+1}{3}\frac{(n+1)n}{2} \\ & = mg\cdot d\frac{(2n+1)(n+1)n}{6}. \end{align}\]The two views should give us the same result, which means
\[\begin{equation} \sum_{i=1}^n i^2 = d\frac{(2n+1)(n+1)n}{6}. \end{equation}\]