Today I Learned
Calculate Sum of Cosines Using Mechanics
Calcualate the sum of
\[\begin{equation} 1 + \cos(2\pi/5)+ \cos(4\pi/5)+ \cos(6\pi/5)+ \cos(8\pi/5). \end{equation}\]We construct a mechanical system with five forces applied to a single point. Each force have stength $1$.
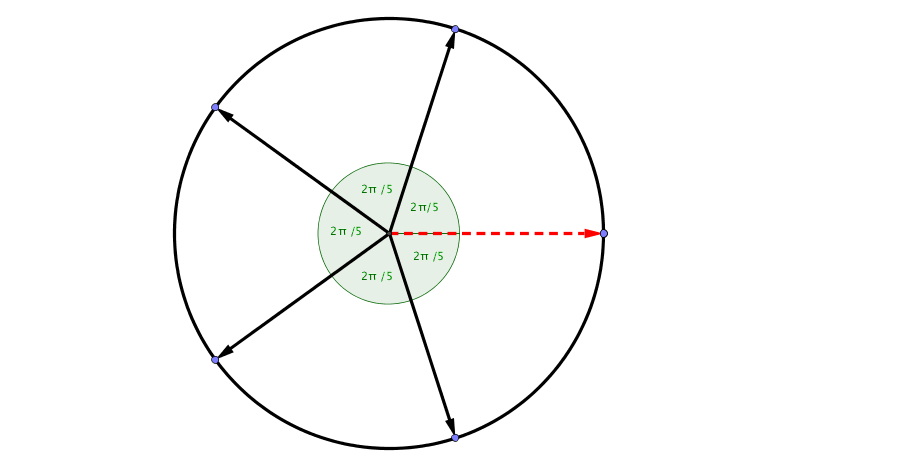
Construct a system with five forces acting on the same point. The file can be downloaded from here
The total force on the horizontal axis is calculated as
\[F_x = 1 + \cos(2\pi/5)+ \cos(4\pi/5)+ \cos(6\pi/5)+ \cos(8\pi/5).\]On the other hand, by symmetry argument, we expect the total force in horizontal axis is zero. The arugment is that if we apply such symmetric forces on an object, it should not move in any direction.
Then we know that
\[\begin{equation} 1 + \cos(2\pi/5)+ \cos(4\pi/5)+ \cos(6\pi/5)+ \cos(8\pi/5) = 0. \end{equation}\]