如何重建宇宙演化历史（未完成）

Alan Sandage 曾经说过 ¹ Cosmology 的任务就是要寻找两个参数：哈勃常数 $H_0$ 和减速因子 $q_0$。这两个分别给出了宇宙膨胀的「速度」和「加速度」。如今我们的技术已经有了很大的进步，同样我们也早已不满足仅仅寻找这两个参数。

The present discussion is only a prelude to the coming decade. If work now in progress is successful, better values for both $H_0$ and $q_0$ (and perhaps even $Λ$ ) should be found, and the 30-year dream of choosing between world models on the basis of kinematics alone might possibly be realized.

一篇 Martin White 的 BAO 讲稿 的扩展笔记。

要重构宇宙演化历史，最基本的是要重构 Hubble 方程，

\[H^2(z) = \frac{8\pi G}{3} \sum\rho_i(z) = H_0^2 \sum \Omega_i(z)\]

其中 $\Omega_i(z) = \rho_i(z)/\rho_ c$ 是能量密度份数，而 $\rho_c = 3 H_0^2 /(8\pi G)$ 是宇宙演化临界密度（即曲率为零）。

因为 Hubble 方程给出的是膨胀历史，所以我们需要有个可以完整描述的距离度量，也就是要有标准尺。为什么不需要标准钟呢？因为我们总可以用红移作为时间度量，然后依据模型给出时间和距离的关系，所以只要有了时间和距离中的一个就可以了，剩下的由理论决定。空间坐标是较为容易测量的量，而时间却会都淹没在历史长河中了。所以我们要使用标准尺。

主要的标准尺有三种：

• Standard Candles
  1. Luminosity distance of well known objects like SN Ⅰa
  2. DAG Differential Ages of Galaxies
• Redshift Drift
• Standard Rulers
  1. BAO Baryon Acoustic Oscillation
  2. Sound wave of early universe

除了标准尺，我们用来了解宇宙演化还会用到 cosmic microwave background, growth of structures (growth index etc)。

Luminosity Distance

Luminosity distance $d_L$ 受到宇宙膨胀历史的影响，

\[d_L = (1+z) \int _ z^0 \frac{\mathrm d\tilde z}{H(\tilde z)}\]

因此只要可以测得大量已知红移的天体的 luminosity distance，我们便可以构造出宇宙的膨胀历史，也就得知了暗能量的状态方程。

但是由于 luminosity distance 是由积分来表示的，所以实际上类似但有差异的状态方程对 luminosity distance 的影响并不是足够大，关于这点可以看到 ² 中的 fig1.

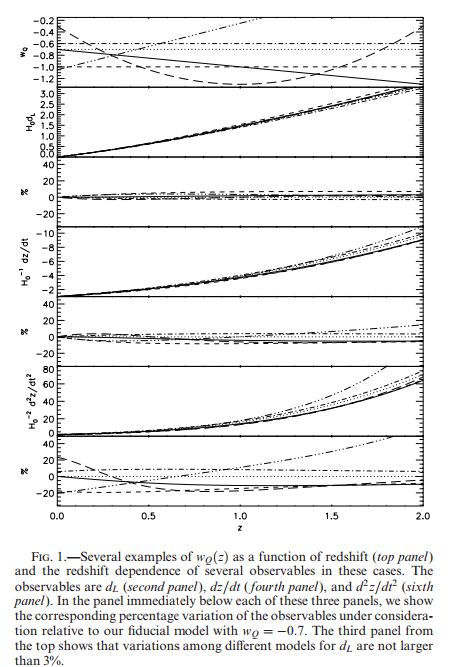
可见对于这些情况的状态方程，红移的高阶导数之间的差异要比 luminosity distance 之间的差异要大多了。

DAG

Hubble 方程 \(H(z) = -\frac{1}{z+1}\frac{\mathrm dz}{\mathrm dt}\) 所以只要能够确定 $\mathrm dz/\mathrm dt$ 即可。

比如如果我们能够找到两个同时形成的天体，而且如果我们能够根据天体的状态得知天体的年龄（e.g., spectroscopic dating of galaxy ages ²），那么我们便可以计算 $\Delta z/\Delta t$ 以估算 $\mathrm dz/\mathrm dt$。通过大量的统计，便可推导出 Hubble 方程和暗能量的状态方程。

因为这是测量红移的一阶导数，从之前的讨论可知，这种方案要比之前的测量 luminosity distance 的方案对不同的状态方程要更加有区分能力。

Redshift Drift

除了 DAG，我们还可以直接测量以我们当地时间为基准的红移变化率，即

\[z(t_0+\Delta t_0) = \frac{a(t_0 + \Delta t_0)}{a(t_s + \Delta t_0)} - 1\]

当 $\Delta t_0$ 很小的时候，我们可以根据导数的定义求的 redshift drift [³]

\(\dot z= \mathrm dz / \mathrm dt_0 =\lim_{\Delta t_0 \rightarrow 0} \frac{\Delta z}{\Delta t_0} = \lim_{\Delta t_0\rightarrow 0} \frac{\dot a(t_0) - \dot a(t_s)}{a(t_s)} = (1+z)H_0 - H(z)\).

在观测方面，我们可以测量星系的退行速度的导数 $\dot v = \Delta v/\Delta t_0$，又因为我们有 $\Delta v = c \frac{\Delta v}{1+z} $

\[\dot v = \frac{c H_0}{1+z} \left(1+z - \frac{H(z)}{H_0}\right)\]

BAO

BAO, baryon acoustic oscillation，是一种非常理想的标准尺。首先，我们可以建立对 BAO 在除了极早期外的整个宇宙历史中的描述。

尾注