The Advection-diffusion Equations

这一部分开始见识到真正的大的体系。首先是一个 Toy model，用到 Advection-Diffusion Equation，平流-扩散方程，即流体的水平运动的相关方程。

7.1 Shallow-fluid and Conservation of Mass

首先了解一下流体的一些基础知识。

假定我们有一个流体体系，我们考虑它的 vorticity $\omega$ 的演化。

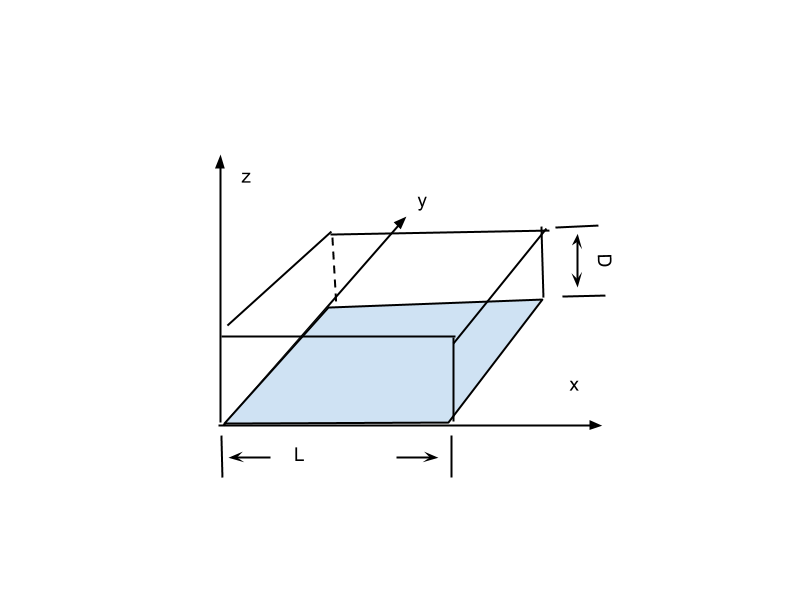
沿着三个坐标轴方向的流体的速度分别是 $u$, $v$, $w$。这样我们定义一个速度矢量 $V$ \(\vec V = \begin{pmatrix} u \\ v \\ w \end{pmatrix}\)

并且定义一个特征量 $\delta = \frac{D}{L}$，我们讨论的情况是 $\delta$ 远小于 1 的情况，这就对应着 shallow fluids.

Shallow fluids 的 vorticity 的定义是这样的： \(\omega = \omega_z = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\)

7.2 The Advection-Diffusion Equation

我们可以根据质量守恒和动量守恒来推导（均匀的不可压缩流体，即密度为常数，不同地方的流体深度相同）流体的另外三个方程：

\begin{eqnarray} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} &=& 0
\frac{\partial u}{\partial t} + 2u \frac{\partial u}{\partial x} + \frac{\partial}{y}(u v ) &=& f v
\frac{\partial v}{\partial t} + 2v \frac{\partial v}{\partial x} + \frac{\partial}{y}(u v ) &=& -f v \end{eqnarray}

化简之后发现其实就是 \(\frac{\partial \omega }{\partial t} + u \frac{\partial \omega }{\partial x} + v \frac{\partial \omega}{\partial y} =0\)

我们可以引入一个特别的函数 $\psi$，stream function，使得 \begin{eqnarray} u &=& - \frac{\partial \psi}{\partial y}
v &=& \frac{\partial \psi }{\partial x} \end{eqnarray}

如此一来，我们的方程就变得更加简单了，例如 \(u_x + v_y = 0\) 是自动满足的。 再比如， \(\omega = \psi_{xx} + \psi_{yy} = \nabla^2 \psi\)

重新整理之前的方程 \begin{eqnarray} \frac{\partial \omega }{\partial t} + [\psi, \omega] &=& v \nabla^2 \omega
\nabla^2 \psi &=& \omega \end{eqnarray} 其中 $[ \psi, \omega ] = \psi_x \omega_y - \psi_y \omega_x$.

7.3 Solution Techniques and Characteristics of Advection-Diffusion

JUST A COMMENT OF THREE KINDS OF SYSTEMS：

PARABOLIC （扩散方程）: $ \frac{\partial \omega}{\partial t} = v \nabla^2\omega $ HYPERBOLIC （波动方程）: $ \frac{\partial \omega}{\partial t} + [\psi, \omega] = 0 $ ELLIPTIC : $ \nabla^2 \omega =0 $