Error Analysis for Time-Stepping Routines
对于科学计算的方法,有两个事情非常重要:
- 计算误差的估计
- 计算的稳定性
这一部分将学习以下几点:
- Truncation Errors (截断误差)
- Local Errors, Global Errors
- Why Higher-order(使用高阶的方法到底有什么好处)
- Numerical Round-off(计算机存储数字的时候会保留某些位数)
- Stability(稳定性)
Truncation Errors of Time-stepping
到现在未知,我们用的方法全是基于 Taylor 展开的,而且我们不是用了所有的展开项,而是用了一部分,也就是我们在某个合适的地方做了截断。
用我们前面使用的 Euler 法来作为例子:
\[y_{n+1} = y_n + \Delta t f(t_n,y_n) + O(\Delta t^2)\]所以在 Euler 法中,我们在 $O(\Delta t^2)$ 处截断。所以,我们可以根据 $\Delta t$ 的大小来估算我们的误差。
Local Error, Global Error
Local Error
\[\epsilon_K = y(t_{K+1}) - [ y(t_K) + \Delta t \phi ]\]即,$t_{K+1}$ 时,真实的 y 值和从 $t_K$ 时刻进行一步预测的 y 值之间的差异。
Glabal Error
\[E_K = y(t_K) - y_K\]即,真实的 y 值与预测的 y 值的差异。全部的,而不是一步的。
可以用 Euler 法作为一个简单的例子。
Euler 法中的 Local Error
\[\epsilon_K = \frac{1}{2} \Delta t^2 \frac{\mathrm d^2 y(c)}{\mathrm dt^2}\]显然,这个 c 是某个值,但是我们并不知道。
Euler 法中的 Global Error
如果我们总共进行了 K 步,那么 global error 应该是
\[E_K = \sum_{j=1}^K \frac{1}{2} \Delta t^2 \frac{\mathrm d^2 y(c_j)}{\mathrm dt^2} = K \frac{1}{2}\Delta t^2 \frac{\mathrm dy(c)}{\mathrm dt}= \frac{b-a}{2}\Delta t \frac{\mathrm d^2y(c)}{\mathrm dt^2}\]这里我们用了几个条件:
- 共进行了 K 步
- 从 a 开始到 b 结束
- 每次的 local error 一样大
Advantages of Higher-order Schemes
对计算机而言,数字的存储是有 round off 的,例如双精度是64位。也就是说,对于我们的计算,某个结果
\[y_{n+1} = y_n^0 + e_{n+1}\]这里 $e_{n+1}$ 就是计算机的 round off.
或者,如果考虑到我们的方法
\[y_{n+1} = y_{n+1}+ E\]$ y_{n+1}$ 是计算机计算过程中保留的值,$E$ 是误差,包含了 round off 和 truncation:
\[E = E_{\text{round}} + E_{\text{truncation}}\]在我们之前的简单 Euler 例子中,
\[E = \frac{e_{n+1} - e_n}{\Delta t} + \frac 1 2 \Delta t \frac{\mathrm d^2 y(c)}{\mathrm d t^2}\]| 考虑到我们有个最大的 $ | e_j | $是 e, |
| $$ | e_{n+1} | \leq e$$, |
| $$ | e_n | \leq e$$, |
并令
\[M = Max|\frac{\mathrm d^2 y(c)}{ \mathrm d t^2} |\]我们就得到了
\[|E| = \frac{2e}{\Delta t} +\frac{1}{2} \Delta t M\]| 画出这个 $ | E | $ 的图像是很有帮助的,我们知道了 $E$ 有一个极小值。可以通过求导来获得 |
时,取得极小。
Stability of Time-stepping Schemes
一个比较简单的例子
\(\frac{\mathrm dy}{\mathrm d t} = \lambda y\) \(y(0)=y_0\)
我们可以解析的得知 \(y(t)=y_0 e^{\lambda t}\)
不过我们要讨论的是计算机计算,所以还是看一下 Euler 方法
\[y_{n+1} = y_{n+t} + \Delta t\lambda y_n = (1+\lambda \Delta t )y_n\]这样经过 N 步, \(y_N = (1+\lambda \Delta t)^N y_0\)
同时我们可以得出误差 \(E = (1+\lambda \Delta t)^N\)
稳定性立判: $|1+\lambda \Delta t|<1$ 时,误差会趋于零,是稳定的。 $|1+\lambda \Delta t|>1$ 时,误差会变成无穷大,不稳定。
General Stability and Implicit Schemes
对于更加一般的 \(y_{n+1} = A y_n\) 的处理。
除了上面的往前算的 Euler 方法(Forward Euler),还有向后算的 Backward Euler 方法。
\[y_{n+1} = y_n + \lambda \Delta t y_{n+1}\]这样我们得到N步之后
\[y_N = \left( \frac{1}{1 - \lambda \Delta t} \right)^N y_0\]这样稳定性正好跟 Forward Euler 的互补。也就是说
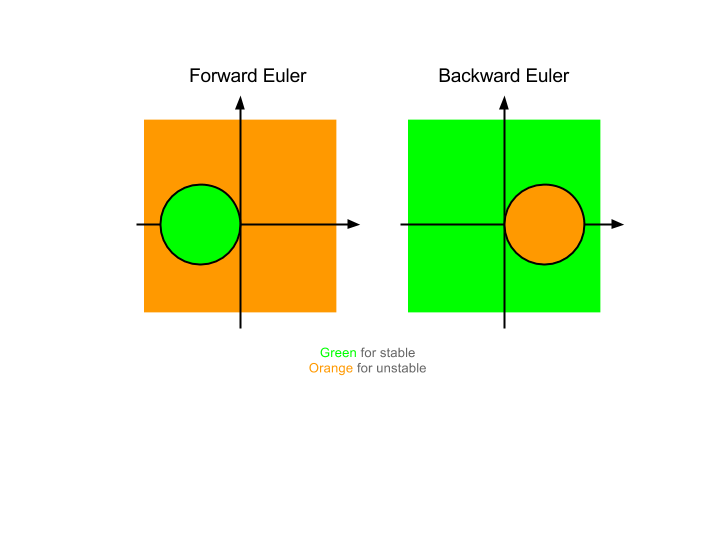
在稳定性区域方面 BE 有着明显的优势。